25. Понятия несмещенности и эффективности оценок параметров модели, понятие состоятельности оценки.

Рассмотрим некоторую случайную переменную y. Пусть - закон ее распределения; здесь символами 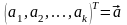обозначены параметры закона.

Объективной основой для оценивания могут служить только наблюденные в опытах начения случайной переменной : .

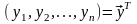Оценки (приближенные значения) параметров и оценка заданной функции этих параметров могут быть вычислены в итоге применения некоторых процедур, соответственно и к результатам наблюдений, т.е.

Предположим, что правило построено и, таким образом, можно вычислить значение 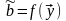. Оно служит функцией случайных переменных и, следовательно, является случайной переменной. Именно в силу данного обстоятельства величина представляет собой лишь оценку величины , т.е. .

Оценка должна удовлетворять определенным требованиям. Самое минимальное требование выглядит так: 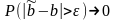при 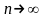, где - сколько угодно малое положительное число. Если удовлетворяет требованию, то называется состоятельной оценкой. Состоятельность означает стремление приближенного равенства к точному равенству по мере увеличения размерности 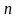выборки .

Если оценка не обладает свойством , то она именуется несостоятельной оценкой, и доставляющая эту оценку процедура рассматривается как непригодная для применения.

Пусть класс заполняют функции переменных , такие, что генерируемые ими оценки величины 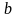непременно удовлетворяют требованию , т.е. .

Пусть функция из класса такова, что дисперсия 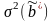оценки 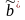, доставляемой функцией , минимальна, т.е. . Тогда оценка называется несмещенной и эффективной, процедура , генерирующая эту оценку, именуется наилучшей в классе , а сам этот класс – классом всевозможных несмещенных процедур оценивания величины .

Если оценка обладает свойствами и лишь в итоге неограниченного увеличения объема выборки , то оценка называется асимптотически несмещенной и эффективной.