21. Последствия нарушения предпосылок теоремы Гаусса-Маркова. (25 баллов)

Изучение последствий нарушения предпосылок теоремы Гаусса-Маркова происходит методом имитационного моделирования.

Для организации процесса получения конкретных значений случайной переменной, обладающей нормальным законом распределения, существуют таблицы конкретных значений стандартных нормально распределенных случайных переменных. Эти переменные обозначим здесь символами . Все переменные в данном наборе являются независимыми, и каждая из них имеет нулевое ожидаемое значение и единичную дисперсию.

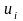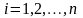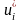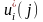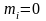Определение значений случайных остатков в ситуации, когда все предпосылки теоремы Гаусса-Маркова адекватны: в эксперименте с номером конкретное значение случайного остатка в уравнении наблюдений с номером определяется в итоге следующих действий: 1. Из столбца таблицы взять в строчке j значение . 2. При и 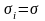для вычислить по правилу .

Определение значений случайных остатков при нарушении равенства нулю их математического ожидания. Значения определяются по правилу , но константы при всех .

Определение значений случайных остатков при нарушении предпосылки гомоскедастичности. Значения определяются по правилу , но величины 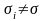при всех .

Нарушение предпосылки о гомоскедастичности случайного порядка влечет следующие негативные для МНК-оценок параметров модели последствия:

1). Оценки коэффициентов утрачивают свойство наименьшей дисперсии, оставаясь при этом несмещенными;

2). Стандартные ошибки оценок коэффициентов перестают объективно отражать точность этих оценок;

3). Оценка параметра 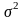утрачивает отчетливый смысл.

Определение значений случайных остатков при нарушении предпосылки об отсутствии автокорреляции. Ниже приведена процедура генерирования значений случайных остатков, которые являются уровнями стационарного временного ряда .

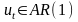Шаг 1. Задаться желаемым значением 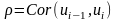коэффициента корреляции случайных остатков 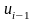и в соседних уравнениях наблюдений. Значение должно удовлетворять неравенству .

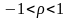Шаг 2. Задаться желаемым значением среднего квадратического отклонения 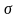случайных остатков.

Шаг 3. Вычислить константу 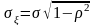. Шаг 4. Определить значение по формуле:

Определение значений случайных остатков и объясняющей переменной при нарушении условия их некоррелированности. Значения определяются по правилу . Однако теперь значения 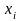объясняющей переменной модели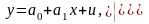 не могут оставаться в каждом эксперименте неизменными. Они должны стать зависимыми от . Значение в эксперименте с номером j обозначим символом . Оно будет вычисляться по правилу 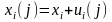, где - значение объясняющей переменной, заданное вне модели. Это правило означает, что для моделирования ситуации нарушения обозначенной предпосылки приходится отказаться от предположения, согласно которому объясняющая переменная принимает свои значения вне модели.

22. Показатели качества регрессии. Коэффициент детерминации как мерило качества спецификации эконометрической модели. (25 баллов)

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.

Для оценки качества модели регрессии используются специальные показатели:

1). Коэффициент детерминации , который служит мерой объясняющей способности регрессоров .

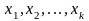2). F-тест, который представляет собой формализованную процедуру проверки статистической гипотезы о полном отсутствии способности регрессоров объяснять значения эндогенной переменной модели.

Смысл коэффициента детерминации как мерила качества спецификации линейной регрессионной модели и процедура его вычисления.

Рассмотрим на примере линейной модели парной регрессии .

Пусть имеется оцененная МНК линейная модель парной регрессии, (1).

Предполагается, что МНК-оценки ее параметров получены по обучающей выборке в ситуации, когда все предпосылки теоремы Гаусса-Маркова адекватны.

В уравнении (1) обозначим символом оценку функции регрессии. Подчеркнем, что регрессор x полностью объясняет левую часть равенства – случайную переменную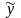 . Следовательно, с учетом и уравнений наблюдений 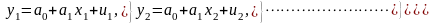справедливы равенства 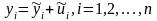. Ясно, что объясняющая способность x тем выше, чем большую долю в переменной y составляет первое слагаемое. Измерить эту долю можно, если привлечь понятие дисперсии.

Согласно свойству операций вычисления дисперсии случайной переменной, операции оценивания дисперсии по выборочным данным справедливо равенство: , где , , , .

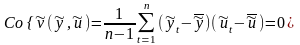Следовательно, в качетсве меры, объясняющей способности регрессора в модели , может служить в пределах обучающей выборки величина .

Она именуется коэффициентом детерминации модели и равна доле эмпирической дисперсии переменной y, которая в рамках обучающей выборки объясняется в модели ее регрессором x.

Коэффициент детерминации всегда находится в промежутке , причем, если , то значения переменной 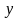полностью объясняются в выборке значениями регрессора .

Напротив, когда , то спецификация модели совершенно плоха, т.к. в рамках такой модели регрессор x абсолютно неспособен объяснять значения переменной y.