19. Процедура интервального прогнозирования по оценённой линейной модели значений эндогенной переменной. (25 баллов)
Дана модель линейной парной регрессии:
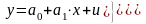
Для
построения интервального прогноза
образуем дробь, имеющую смысл нормированной
ошибки прогноза:
,
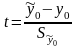где
-
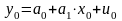модель линейной парной регрессии,
-
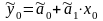точечный прогноз величины
,
-
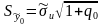средняя квадратическая ошибка прогноза
в которой
.
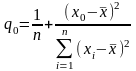Если
случайный остаток в модели не имеет
автокорреляции и нормально распределен,
то эта дробь обладает законом распределения
Стьюдента с числом степеней свободы
,
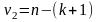где k+1
– количество оцениваемых коэффициентов
модели. Так, для нашей модели k+1=2.
На
основании этого утверждения можем
записать равенство
,
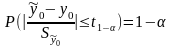где
.
Данное
обстоятельство позволяет построить
замкнутый промежуток
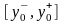с
границами
,
,
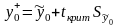именуемый доверительным
интервалом,
который накрывает прогнозируемое
значение
с принятой доверительной вероятностью
.
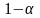Тут символом
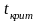обозначено
критическое значение модуля дроби
Стьюдента (двусторонняя (
)-квантиль
распределения Стьюдента), которую удобно
рассчитывать по величинам
,
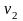при
помощи функции СТЬЮДРАСПОБР.
20. Модели нестационарных временных рядов с трендом и сезонной составляющей и их идентификация.
Модель
тренда выглядит следующим образом:
,
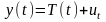где t – время; T(t) - временной тренд
заданного параметрического вида
(например, линейный
);
- случайная (стохастическая) компонента.
Модель
сезонности:
,
где S(t) - периодическая (сезонная)
компонента,
-
случайная (стохастическая) компонента.
Модель тренда и сезонности, именуемая аддитивной, имеет следующую предварительную спецификацию:
,
,
.
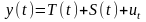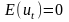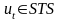Следовательно,
в модели функция регрессии
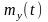уровней
ряда
на
переменную времени t
представлена суммой тренда
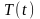и
сезонной составляющей
.
Случайный остаток
предполагается
некоторым стационарным рядом с нулевым
ожидаемым уровнем. Спецификация требует
конкретизации функций
,
и
модели
.
В
качестве модели
примем
модель авторегрессии первого порядка
- AR(1).
Эта модель включает два независимых
параметра
.
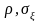Функция
является
периодической с целочисленным периодом
.
Период
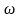соответствует
одному году; например
,
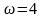если единичный отрезок времени равен
одному кварталу. В качестве функции
выбираем
линейную комбинацию фиктивных переменных
.
Так что
.
Промежуток t,
в котором все фиктивные переменные
равны
нулю, именуется базовым периодом. Если
t
соответствует базовому периоду, то
.
Чтобы
осуществить выбор функции
из
некоторого множества
возможных
вариантов, нужно сопоставить наблюдаемые
проявления тренда
исследуемого
ряда с соответствующими проявлениями
каждого элемента
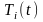множества
F.
Ту альтернативу
,
наблюдаемое проявление которой («след
когтя») ближе всего к соответствующему
проявлению тренда моделируемого ряда,
и следует выбрать в качестве модели
тренда.
Таким образом, уточненная модель нестационарного временного ряда с трендом и сезонной составляющей:
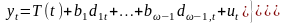
Данная модель нужна для объяснения уровней ряда , значениями переменной времени t.