17. Теорема Гаусса-Маркова, основные допущения и предпосылки, их практическое содержание и назначение. (25 баллов)

Теорема Гаусса-Маркова.

Пусть матрица X уравнений наблюдений имеет размер 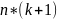, где 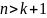, и обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют четырем условиям:

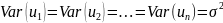
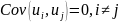
Тогда:

а) Наилучшая линейная процедура 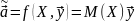имеет вид:

б) Эффективная линейная несмещенная оценка обладает свойством наименьших квадратов:

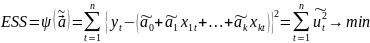
в) Ковариационная матрица оценки вычисляется по правилу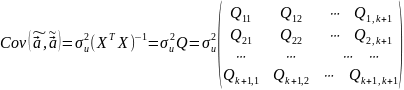

г) Несмещенная оценка параметра 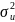модели находится по формуле ,

где n – число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели.

Предпосылки теоремы Гаусса-Маркова.

Если факторы (объясняющие переменные) уравнения неслучайны и линейно независимы,

а остатки уравнения

1. Случайны

2. Имеют нулевое математическое ожидание для всех наблюдений

3. Имеют постоянную дисперсию

4. Неавтокоррелированы

ТО несмещённые и эффективные оценки параметров уравнения регрессии можно получить

методом наименьших квадратов. Нарушение одного из условий Гаусса-Маркова приводит к нарушению эффективности оценок, т. е. в классе несмещенных оценок можно найти такие, которые имеют меньшую дисперсию.

Тестируемые предпосылки теоремы Гаусса-Маркова:

1. О гомоскедастичности случайного остатка в модели (тест Голдфелда-Квандта);

2. О некоррелированности случайных остатков в уравнениях наблюдений (тест Дарбина-Уотсона).

18. Случайная переменная (дискретная и непрерывная) и закон её распределения. (15 баллов)

Пусть 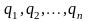- набор некоторых различных констант. Соберем их в множество .

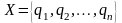Рассмотрим величину x, которая может принимать любые значения из множества X. Такая величина x называется переменной, а множество X – множеством ее возможных значений.

Переменная величина x с областью изменения X называется случайной, если свои возможные значения q из множества X переменная x принимает в результате некоторого опыта со случайными элементарными исходами вида 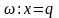. Это элементарное событие означает, что переменная величина x в опыте приняла значение q.

Случайная переменная x именуется дискретной случайной переменной, если множество X состоит из конечного или счетного количества констант 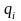. Случайная переменная x именуется непрерывной случайной переменной, если множество X является промежутком числовой прямой 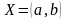и вероятность каждого элементарного исхода равна нулю.

Полной характеристикой случайной переменной x служит ее дифференциальный закон распределения. Так называется функция скалярного аргумента q, определенная из всей числовой прямой, характеризующая объективную возможность появления в опыте значений q случайной переменной x.

Если x – дискретная переменная, то

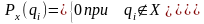
Следовательно, 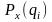- это вероятность появления в опыте значения случайной переменной x. Эта функция именуется вероятностной функцией дискретной случайной переменной x. Значения функции неотрицательны и обладают следующим свойством .

Дифференциальный закон распределения непрерывной случайной переменной x, если этот закон существует, имеет более сложный смысл:

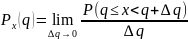
и называется плотностью вероятности. Значения функции неотрицательны и обладают свойством

.