14. Тест Дарбина – Уотсона отсутствия автокорреляции случайного остатка в линейной модели множественной регрессии. (15 баллов)

Для проверки на автокорреляцию используется тест Дарбина-Уотсона.

Выдвигается гипотеза об отсутствии автокорреляции в остатках: 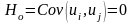при .

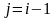Вычисляем критерий Дарбина-Уотсона: ,

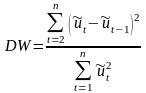где 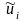- оценки случайных остатков .

Областью изменения переменой DW служит интервал (0,4).

По таблице Дарбина-Уотсона определяем критические значения критерия Дарбина-Уотсона 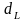, для заданного числа наблюдений n и числа объясняющих переменных k. По этим значениям разбивают промежуток (0,4) на 5 отрезков. И проверяется, в какое множество попала величина DW.

При попадании статистики DW в множество принимается альтернативная гипотеза при .

Если статистика DW попадает в множество 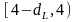, то принимается альтернативная гипотеза

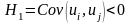при .

Когда статистика DW попадает в зону неопределенности, то ни отклонить, ни принять гипотезу при помощи данного теста не удается.

15. Отражение в модели влияния на эндогенные переменные неучтённых факторов. Приведённая форма эконометрической модели. (15 баллов)

Именно случайные возмущения отражают в модели воздействие на эндогенные переменные неучтенных факторов. Такие модели принято называть регрессионными моделями.

Обратимся к спецификации «паутинной» модели спроса-предложения товара на конкурентном рынке:

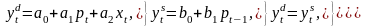
В первом уравнение уровень текущего спроса 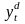определяется текущей ценой товара и текущим доходом потребителя. На текущий спрос оказывают влияние и другие факторы. Например, ожидаемый уровень душевого дохода потребителя в следующем периоде, 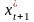. Этот фактор в спецификации модели отсутствует, т.е. является неидентифицированным. Однако отсутствие в спецификации модели каких-то факторов вовсе не избавляет от их влияния на эндогенные переменные модели.

Отражение в спецификации модели влияние на текущий спрос (предложение) неучтенных факторов происходит путем включения в поведенческие уравнения модели случайных переменных, значения которых рассеяны вокруг нуля. Такие случайные переменные называют случайными возмущениями или остатками. Вот так выглядит спецификация «паутинной» модели спроса-предложения товара после включения в уравнения случайных возмущений, соответственно и :

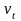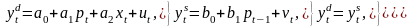
Рассеянные вокруг нуля случайные переменные и отражают влияние на текущие эндогенные переменные этой модели ,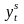 , 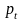неучтенных факторов. Расположенная в правой части первого уравнения линейная функция называется функцией регрессии. Аналогично во втором уравнении.

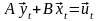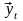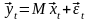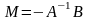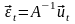Представим спецификацию модели в компактном виде: , где - вектор случайных возмущений, и - векторы соответственно текущих эндогенных переменных и предопределенных переменных моделей. В свою очередь, компактная запись приведенной формы модели имеет вид: , где - матрица коэффициентов приведенной формы модели, а - вектор случайных возмущений в приведенной форме модели.