7. Принципы моделирования экологических процессов и их реализация в модели «хищник-жертва» и модели озерной экосистемы.

Принципы моделирования экологических процессов

Любая биосистема, включающая совместно функционирующие организмы на данном участке и взаимодействующая с физ средой т.о., что поток энергии создает четко опред. биоструктуры и круговорот вещ-в м/у живой и неживой частью, предст собой экосистему. Специфические особенности: - сложность внутр строения, - полифакторность внешней среды, - незамкнутость, - нелинейность. Вследствие этого – фазовое пространство многомерно, - мат модель содержит много параметров, - нбх совместное моделирование биосистемы и среды функционирования, - разный характер нелинейности.

В основе мат модели – логические схемы моделей, предмодели. Принципы:

1) полнота описания – д б ясно, какой элементарный акт вып

2) принцип «развивающейся» модели – блочная структура модели, возможность ее наращивания

3) иерархия моделей – популяционный и биогеоценотич уровни

4) системный подход – БГЦ как система, потоки субстанций из блоков, интенсивность субст – их кол-во, котор переносится из блока, подсчит баланс

5) сотрудничество естествоиспытателей и математиков – составление схемы, постр модели, анализ рез-тов.

6) информационное обеспечение

Модель «хищник-жертва»

1. жертва размножается экспоненциально в отсутствие хищника

2. в отсутствие жертвы популяция хищника экспоннциально вымирает

3. суммарное кол-во биомассы жертв, потребляемое популяцией хищника, линейно зависит от плотности популяции жертвы и от плотности популяции хищника,

4. потребленная хищником биомасса жертвы перерабатывается пост коэф в биомассу хищника

5. доп факторы отсутствуют

В этих предположениях модель может быть записана в виде:

где - плотность популяции жертвы; - плотность популяции хищника; - скорость размножения популяции жертвы в отсутствие хищника; - естественная смертность хищника; - удельная скорость потребления популяцией хищника популяции жертвы при единичной плотности обеих популяций; - коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу.

Проанализировав данную систему, можно сформулировать следующие законы:

- закон периодического цикла: колебания численности двух видов периодичны. Для некоторой пары значений численностей состояние биологического сообщества стационарно и равновесие устойчиво.

- закон сохранения средних: средние в течение периода T численности особей двух видов не зависят от начальных условий и равны числам, соответствующим нетривиальному стационарному состоянию для данных значений параметров .

- закон изменения средних: если два вида истребляются равномерно и пропорционально численности особей, то среднее число жертв возрастает, а хищников- убывает.

Опыт, накопленный при обобщении моделей математической экономики и экологии, позволил перейти к построению комплексных эколого- экономических моделей, в состав которых входят два основных блока, описывающих экономические и экологические процессы. При этом каждый блок обязательно содержит уравнения, связывающие переменные экологической и экономической подсистем между собой.

По уровню агрегированности эколого-экономические модели можно разделить на региональные и глобальные.

Региональные, как правило, концентрируют внимание на некоторой проблеме, определяемой спецификой отдельного региона. В модели с наибольшей полнотой описываются процессы, имеющие непосредственное отношение к рассматриваемой проблеме. Возможны и региональные модели общего назначения.

Глобальные модели описывают функционирование мировой экономики и ее воздействие на биосферу. Как правило, они имеют иерархическую структуру, включая в качестве блоков модели крупных регионов мира. В числе биосферных процессов рассматриваются глобальные биогеохимические циклы, динамика атмосферы и Мирового океана, прирост органического вещества и растительности. Экономическую подсистему характеризуют процессы производства и потребления, демографические процессы, загрязнение окружающей среды и т. д.

Отличительной чертой эколого- экономических моделей является их управляемость - наличие свободных экзогенных переменных, значения которых исследователь может задавать по своему усмотрению. Обычно наборы значений объясняющих переменных объединяются в сценарии, отображающие различные стратегии управления изучаемыми эколого- экономическими системами. Качественный анализ фазовых траекторий изучаемой системы при различных сценариях развития позволяет оценить допустимость этих сценариев с социально- экономической и социально- экологической точек зрения.

Как правило, эколого-экономические модели имеют блочную (модульную) структуру, т. е. состоят из сравнительно автономных подсистем (блоков), описывающих соответствующие компоненты эколого- экономической системы. Структура модели должна позволять при необходимости наращивать число блоков, учитывая новые факторы или сведения.

Различные блоки могут формироваться с помощью различного математического аппарата: дифференциальных, интегральных и разностных уравнений, систем алгебраических уравнений и неравенств и т. д.

---------------------------------------------------------------------------------

Модель озерной экосистемы (представляет концептуальную модель процесса эвтрофикации – высокая концентрация орган биомассы)

Фазовые переменные:

-фитопланктон – a(t),

-зоопланктон – z(t),

-концентрация питательных веществ – n(t),

-масса детрита – s(t),

-биомасса бактерий – b(t),

-концентрация кислорода – x(t).

Динамика этих веществ оказывает решающее воздействие на состояние экосистемы.

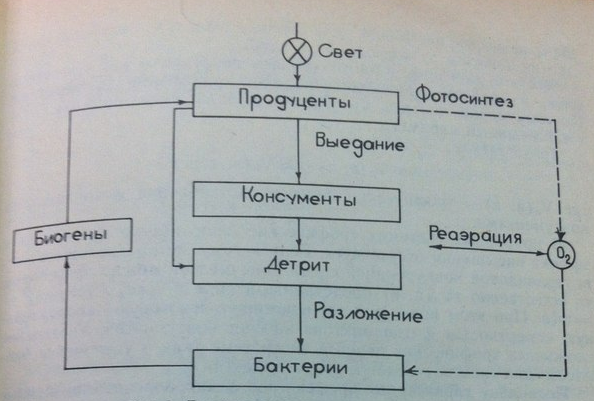
---Продуценты(фито)Консументы(зоо) выедают(реаэрация)ДетритРазложениеБактерии---Биогены---

Балансовые ур-ния

Da/dt=q(na)-q(az)-q(as)

Dz/dt=q(az)-q(zs) – малая вел

Ds/dt=q(as)+q(zs)-q(sb)

Db/dt=q(sb)-q(bn)

Dx/dt=k(x(n)-x)+q(xa)-q(xb),

Где k-коэффициент реаэрации, q(ij) – поток вещества из I блока в J, x(n) – концентрация кислорода.

Сильно агрегирована(неправдоподобно), из-за этого результаты носят сугубо качественный характер и не годятся для конкретных прогнозов. В итоге им закон сохр вещ-ва – a+n+s=A=const – опред скорость и степень эвтрофикации; две стационар точки системы 1) a1*=0,s1*=0, x1*=x(mu), n1*=A; 2) a2*=B*mu/[(p+mu)(alfa-ro)], s2*=B*ro/(ro+mu)(alfa-ro), mu=f(x2*)

Модификации вольтеровских моделей: 1) продолжение исследований, 2) отрицание – более точное описание действительности, 3) исследование новых проблем в экологии

В наст вр не сущ-ет др моделей биолог сообществ, достаточно общих для объяснения з-номерностей динамики составляющих сообщество популяций, и в то же время конкретных и простых.