14. Структура модели моБа с учетом природоохранного фактора в. Леонтьева. Анализ модели с точки зрения соответствия требованиям к моделям, описывающим экологически устойчивое экономическое развитие.

Межотраслевая балансовая модель макроэкономики В. Леонтьева с учетом атмосфероохранных мероприятий строится на рассмотрении природоохранных мероприятий в качестве «чистой отрасли» межотраслевого баланса.

Выделение очистных мероприятий позволяет определить:

• объем средств, отвлекаемых от непосредственного производства на охрану природы, и зависимость между их величиной и уровнем производственного развития;

• участие отраслей в природоохранных мероприятиях;

• экологическую целесообразность каждого направления в материальном производстве;

• связь между совершенствованием технических средств очистки и затратами на него.

Целесообразность рассмотрения очистных мероприятий в межотраслевом разрезе вытекает из их тесного взаимодействия со всем народным хозяйством. Каждая отрасль связана с деятельностью по очистке через выпускаемые и направляемые на очистные сооружения производственные отходы.

Признание необходимости и возможности выделения очистных мероприятий в структуре межотраслевого баланса ставит конкретные вопросы относительно форм расширения модели.

Модель Леонтьева формулируется следующим образом:

Где А₁₁- матрица коэффициентов а_ij, характеризующих величину поставок i-го продукта для производства единицы j-го продукта без учета затрат на ликвидацию загрязнителей; А₂₁- матрица коэффициентов a_gj, характеризующих количество g-го вредного вещества, сопутствующее выпуску единицы продукции j-й отрасли ; А₂₂- матрица коэффициентов a_gk, характеризующих количество вредного вещества g-го вида, сопутствующее ликвидации единицы к-го загрязнителя ; Х₁ – вектор валовых выпусков отраслей материального производства; У₁ – вектор конечного продукта ; Х₂ – вектор ликвидированных масс различных вредных веществ; А₁₂- матрица коэффициентов а_ij, характеризующих затраты продукта i-й отрасли, необходимые для обезвреживания единицы g-го загрязнителя; У₂ – вектор выпуска вредных веществ в биосферу.

Основным измерителем в блоке очистных мероприятий и выпуска загрязняющих среду отходов модели Леонтьева служит масса загрязнителей. Но использование такого параметра связано с преодолением ряда трудностей.

Во-первых, эта величина может быть исчерпывающей характеристикой вредности лишь в случае равномерного распределения загрязнителя в среде независимо от характера выброса. Однако для равномерного распределения требуется достаточно длительное время, особенно если речь идет о сбросе вредных веществ в водоемы. Поэтому санитарные нормы спуска сточных вод в водоемы, которые в модели Леонтьева включены в вектор конечного продукта, измеряются в настоящее время показателем концентрации загрязнителей, а не их массы.

Во-вторых, масса вредных веществ должна находиться в прямой зависимости от других параметров модели. Блок отчистки должен линейно соотноситься с объемами производства продукции. Показатель массы этому условию не соответствует, что обнаруживается при анализе связи между объемом обезвреживаемых загрязнителей и межотраслевыми поставками продуктов, необходимых для процесса очистки.

Модель Леонтьева построена в предположении, что затраты на очистные мероприятия прямо пропорциональны массе обрабатываемых загрязнителей, т.е. стоимость обезвреживания единицы каждого загрязнителя постоянна. В действительности же существенна зависимость затрат на очистку от концентрации обрабатываемого раствора. Функция затрат на очистку может быть построена от разных аргументов. В качестве аргумента используют, в частности, степень обезвреживания отходов, изменяющуюся от нуля до единицы. На этом отрезке функция затрат является неубывающей и, существенно нелинейной, т.е. затраты на обезвреживание единицы массы изменяются под влиянием концентрации.

Проверка требований

1) не вып, т.к. модель линейна, хоть и ориентирована на достаточно длительный временной интервал,

2) учитывает влияние экономической деятельности на природные процессы и условия, что выражено в матрицах выбросов вредных веществ A21, A22;

3) включены потоки обратной связи между экологической и экономической подсистемами эколого-экономической системы, выражено в матрице коэф обезвреживания загрязняющих веществ A12;

4) не вып, поскольку не включены нематериальные аспекты

5) нет в явном виде ограничений на природный капитал, загрязнение и экономический капитал для гарантии равномерного распределения природного и экономического потенциала между последующими поколениями;

6) нет возможности описания качественных структурных изменений;

15. Балансовая межотраслевая макроэкономическая модель с включением водоохранного фактора. Предпосылки построения и структура модели, этапы практического построения. Анализ результатов экспериментальных расчетов. Анализ модели с точки зрения соответствия требованиям к моделям, описывающим экологически устойчивое экономическое развитие.

В этой модели делается попытка дополнить классическую модель межотраслевого баланса переменными и связями, характеризующими водохранные мероприятия. В основу построения модели положены следующие предпосылки:

1) Основой объединения процессов производства продукции и очистной деятельности в «чистые отрасли» служит однородность технологических процессов. Производство выпускает, как правило, многокомпонентные стоки, т. е. содержащие несколько вредных веществ. Состав стоков, содержащих одно и то же загрязняющее вещество, но выпускаемых разными отраслями, существенно различен по содержанию ингредиентов, поэтому неодинаковы и технология очистки, и связанные с ней затраты.

2) В модели используется показатель концентрации загрязнителей, а не их массы.

3) Зависимость затрат на очистку от объема обрабатываемого стока принимается линейной с той же точностью, что и для всех отраслей народного хозяйства. Делается допущение об отсутствии загрязняющей деятельности самой отрасли очистки.

Такую модель следует строить на основе детализации очистных мероприятий в разрезе сточных вод каждой отрасли. При этом число строк и столбцов в матрице коэффициентов баланса удваивается: добавляются строки, соответствующие каждой отрасли, и столбцы водных стоков.

Такая классификация однозначно определяет и систему показателей: объем стоков, выпускаемых при производстве единицы продукции каждой отрасли, и затраты на обезвреживание единицы объема соответствующих стоков до уровня, определяемого санитарными нормами содержания вредных веществ в водоеме.

Обозначим через объем сточных вод i- й отрасли, выпускаемой при производстве единицы продукции вида i и поступающей на очистные сооружения. В матрицу технологических коэффициентов МОБ введем n векторов-строк вида , указывающих объемы стоков каждой отрасли на единицу продукции. Дополнительные столбцы указывают в межотраслевом разрезе затраты на обезвреживание сточных вод. Коэффициенты означают затраты продукта i- й отрасли, необходимые для очистки единицы объема стока j- й отрасли до санитарных норм спуска сточных вод в водоем.

Вектор валового выпуска X расширяется координатами , определяющими весь объем стоков i- й отрасли: .

Получаем следующую схему расширенного межотраслевого баланса:

(3.5)

где - матрица коэффициентов , характеризующих поставки i- го продукта для производства единицы j- го продукта без учета затрат на очистку стоков j-й отрасли; G- матрица коэффициентов ; - диагональная матрица коэффициентов ; Y- вектор конечного продукта.

Рассмотрим балансовые уравнения в приведенной схеме модели:

(3.6)

Смысл уравнения первого вида состоит в том, что валовой выпуск i- й отрасли должен покрыть спрос на i- й продукт со стороны всех n отраслей материального производства, потребности процессов очистки стоков всех отраслей и заданный конечный продукт . Уравнения второго типа определяют весь объем стоков, выпускаемых отраслью i.

В этой модели параметром, регулирующим качество окружающей среды, служит величина затрат на очистку единицы стока . В зависимости от стандартов качества среды будут изменяться затраты на очистные мероприятия, а следовательно, и структура и валовые выпуски всех отраслей материального производства.

Исследуем матрицу технологических коэффициентов модели. От матрицы A традиционной схемы межотраслевого баланса мы перешли к матрице

, (3.7)

балансовое уравнение

(3.8)

преобразовали в систему уравнений

(3.9)

В обычной модели МОБ межотраслевые поставки продуктов для очистки стоков отрасли учитывались вместе с поставками продуктов, непосредственно идущих на производство основной продукции данной отрасли. В системе же (3.9) введена отдельная позиция для отрасли очистки.

Таким образом, система (3.9) есть модель типа (3.8), сформулированная по отдельности в пространствах векторов X и V.

Запишем (3.9) иначе:

(3.10)

откуда следует, что

(3.11)

Экономический смысл этого равенства состоит в том, что выделение в МОБ деятельности по очистке ведет к изменению матрицы коэффициентов прямых затрат для всех отраслей. Очевидно, коэффициенты прямых затрат i- й отрасли должны уменьшиться на величину средств, необходимых для обезвреживания объема стока, сопутствующего выпуску единицы продукции j- й отрасли:

(3.12)

Этапы практического построения:

I. Разработка классификации модели с целью выделения в ней тех отраслей, суммарные затраты на очистку стоков которых наиболее значительны. Эти затраты определяются объёмом очищенных стоков и себестоимостью очистки 1м³ этих стоков.

II. Формирование коэффициентов, отражающих процесс очистки в межотраслевом резерве в соответствии с выбранной классификацией отраслей.

III. Пересчёт коэффициентов прямых затрат на производство основной продукции отрасли. Затраты на очистку включены в себестоимость основной продукции отрасли, поэтому из вектора коэффициентов прямых затрат каждой отрасли следует вычесть соотв.вектор коэффициентов затрат на очистку 1м³ стоков, умноженный на коэф.объёма очищенных сточных вод от производства единицы продукции отрасли.

Результат расчётов по такой расширенной модели – величина фактических затрат на очистные мероприятия. Чтобы определить масштаб производственной деятельности, при которой будет поддерживаться нормативное состояние окруж.среды, необходимо построить матрицу коэффициентов затрат на очистку сточных вод предприятиями, соблюдающими экологические нормативы.

Анализ модели с точки зрения соответствия требованиям к моделям, описывающим экологически устойчивое экономическое развитие.

1. – (линейная зависимость)

2. +

3. + (зависимость структуры и объёма выпуска от заданного состояния окружающей среды)

4. + (величина затрат на очистные мероприятия зависит от уровня нормативного состояния окр.среды)

5. + (Коэффициенты означают затраты продукта i- й отрасли, необходимые для очистки единицы объема стока j- й отрасли до санитарных норм спуска сточных вод в водоем)

6. –

7. – (не учитывает ограниченности природных ресурсов)

16. Применение модели межотраслевого баланса для оценки эффективности водопотребления и экспорта воды в российской экономике. (необходимо выделить для себя что-то главное, т.к. переписать все это никакого времени не хватит)

Для определения эффективности экологической политики и снижения использования ресурсов на единицу продукции обязательная полная и достоверная информация о взаимосвязях между экономической системой и ОС, для чего необходимы адекватные инструменты и индикаторы.

• Анализ потоков и ресурсов

Признан ЕС в качестве основного инструмента анализа экологической эффективности.

В России недостаток данных затрудняет введение этого метода, который необходим как при принятии решений на микро- и макро-уровнях, при осуществлении экологического контроля и аудита.

• Модель межотраслевого баланса

-позволяет вычислить как прямые потоки ресурса, потребляемого отраслью в процессе производства для удовлетворения своего ассортиментного вектора, так и косвенные, вызванные потреблением продукции других отраслей.

Рассмотрим применение модели отраслевого потребления воды, комбинирующей модель межотраслевого баланса Леонтьева с моделью использования энергии.

• Рассмотрим основные уравнения межотраслевого баланса

Существует некоторая экономическая система, состоящая из n отраслей. Согласно основным уравнениям в модели Леонтьева, производство в экономике зависит от межотраслевых отношений и окончательного спроса, или ассортиментного вектора (у1 ,....,уn).

Пусть Xij – часть продукции отрасли i, потребляемой отраслью j в процессе производства

• Соответствующая система уравнений может быть записана следующим образом:

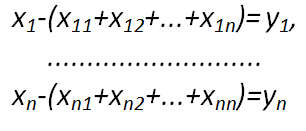
Коэффициенты прямых затрат или технические (технологические) коэффициенты производства aij определяются как затраты продукции отрасли i, используемые отраслью j на изготовление единицы ее продукции:

aij = xij/xj

Тогда x=Ax+y. Решая уравнение относительно х, получаем: х= (Е-А)^-1y, где (E-A)^-1-обратная матрица Леонтьева, определяющая продукцию х, которую каждая отрасль должна произвести для удовлетворения ассортиментному вектору у экономики.

Следовательно, производство в отрасли i можно представить следующим образом:

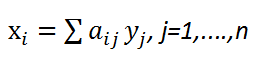
где aij – увеличение производства в отрасли i, если спрос отрасли j на продукцию отрасли i увеличивается на одну единицу.

• Переменные модели

• w_d – вектор реального потребления воды;

• w_di – вода, потребляемая непосредственно отраслью i(куб.м);

• w_l – вектор полного потребления воды;

• w_li – полное потребление воды отраслью i ;

• W-матрица межотраслевых водных отношений;

• w_ij – элемент матрицы W, определяющий количество воды, потребляемое отраслью i для производства продукции, потребляемой отраслью j в своем производственном процессе;

• Q - матрица технических коэффициентов для воды, учитывающая прямое потребление воды;

• q_ij – элемент матрицы Q, определенной как технический коэффициент водного потребления, который выражает отношение «закупок» воды отраслью j у отрасли i к полным «закупкам» воды отрасли j ;

«Закупки» воды отраслью j у отрасли i- количество воды, потребляемое отраслью i для производства продукции, потребляемой отраслью j ;

• (E-Q)^-1- обратная матрица Леонтьева для воды, элементы которой определяются как дополнительное ее количество, которое отрасль i будет потреблять, если спрос на воду отрасли j увеличится на одну единицу. Матрица учитывает полное потребление воды;

• w^y_di – количество воды, потребляемой непосредственно отраслью i для удовлетворения спроса, внешнего по отношению к рассматриваемым отраслям, или ассортиментного вектора экономики;

• w^*_d – вектор-индикатор прямого потребления воды на единицу произведенной продукции;

• w^*_dl – индикатор прямого потребления воды на единицу произведенной продукции отраслью i(куб.м/руб) ;

• w^*-вектор- индикатор полного потребления воды, или изменение в общем объеме потребленной отраслями воды, при изменении на единицу спроса любой заданной отрасли;

• w^*_ind – вектор- показатель косвенного потребления воды или разность между индикаторами полного и прямого потребления воды (w^*_i -w^*_dl);

• w^*_i – индикатор полного потребления воды отраслью i ;

• wm – вектор- индикатор полного потребления воды;

• im – вектор- показатели косвенного потребления воды ;

Потребление воды представляет собой объем воды, используемой отраслью, минус ее сброс.

Основное уравнение Леонтьева может быть выражено в терминах потребления воды: количество воды, непосредственно потребляемой отраслью i (реальное потребление), зависит от межотраслевых отношений, установленных между этой отраслью и другими отраслями, и от количества воды, потребляемой отраслью i при производстве продукции для удовлетворения конечного спроса:

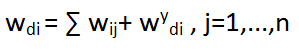
• Множество технических коэффициентов водного потребления

q_ij , или количество воды, потребляемой отраслью j при производстве продукции, потребляемой отраслью i, по отношению к общему количеству воды, потребляемой отраслью j : q_ij=w_ij/w_dj=w^*_di a_ij/w^*_dj, j=1,...n.

Диагональные элементы матрицы технических коэффициентов q_ij повторяют a_ij

Тогда w_d=Qw_d + w^y_d , где Q-кв.матрица техн.коэффициентов потребления воды с элементами qij.

• Из уравнения получаем выражение, определяющее модель водного потребления

w_d=(E-Q)^-1w^y_d ,где (E-Q)^-1 обратная матрица Леонтьева для потребления воды, определяющая его изменение, если спрос на нее изменится на единицу, а элементы этой матрицы указывают на дополнительное количество воды, потребляемой экономической системой в целом, когда отрасль j увеличивает свой спрос на одну единицу.

Можно вычислить индикатор прямого потребления на производственную единицу (w^*_d), или количество воды, потребляемое непосредственно каждой отраслью на единицу производственной продукции, представленное вектором, каждый элемент которого определен по формуле: w^*_di=w_di/x_i

Полное потребление воды может быть найдено как количество воды, потребленное на единицу произведенной продукции, умноженное на количество произведенной каждой отраслью продукции:

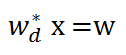
Выразим вектор производства х согласно модели Леонтьева. Предыдущее уравнение перепишем как

где w- полное потребление воды экономической системой, а - вектор, каждый элемент которого определяет количество воды, потребляемой и прямо, и косвенно, если спрос какой-нибудь отрасли и изменится на одну единицу, или индикатор полного потребления воды:

• Косвенное потребление воды на единицу продукции:

w^*_ind=w_i^*-w_di^*

Индикатор прямого потребления воды(wm) показывает, как увеличивается общее потребление воды при увеличении спроса в какой-либо отрасли: wm_i=w_i^*/w_di^*

Т.о., wm определяет отношение полного объема воды, потребляемой на каждую единицу производственной продукции к количеству воды, потребляемой прямо при производстве единицы продукции.

• Показатель косвенного потребления воды (im)

im_i= wm_i -1 = (w_i^*/w_di^*) -1

Этот показатель определяет, сколько воды потребляется косвенно данной отраслью на каждую единицу воды, используемую напрямую.

Обозначив элементы матрицы (E-Q)^-1 через β_ij, получим матрицу межотраслевого потребления воды W:

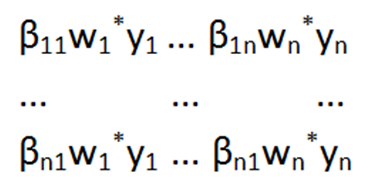
В этой матрице сумма элементов каждого столбца обозначает для соответствующей отрасли j полное потребление воды этой отраслью w_ij для соответствия ассортиментному вектору экономики, а общее потребление воды всей экономической системой в целом можно выразить как скаляр w_i=∑w_ij .

• Потребление воды в разрезе основных отраслей экономики России.

Для расчета прямого потребления воды на единицу продукции использовались данные системы таблиц «Затраты-выпуск» России за 2002 год, выпущенные Федеральной службой государственной статистики в 2005 году.

• Реальное потребление воды и отечественная продукция в 2002г.

• 

Как видно из данных, представленных в таблице, основные потребители воды из промышленности- электроэнергетика(4281.6 млн.куб.м) , деревообрабатывающая и целлюлозно-бумажная (1394.8 млн.куб.м), химическая и нефтехимическая(1069.8 млн.куб.м)

• Индикаторы потребления воды в 2002 г.

• 

• Индикатор прямого потребления воды для каждой отрасли отражает отношение полного потребления воды в отрасли на единицу продукции к количеству воды, потребленной прямо на единицу продукции.

• Показатель косвенного потребления воды для каждой отрасли определяет, сколько воды используется косвенно данной отраслью на каждую единицу воды. используемую прямо, для удовлетворения спроса на продукцию данной отрсли.

• Пищевая промышленность, например, как мы видим из данных второй таблицы, на каждый куб.м потребленной прямо воды потребляет косвенно 9.13 куб.м, угольная промышленность-6.57, строительных материалов- 3.63, легкая-3.52.

• При увеличении прямого потребления воды в данных отраслях за счет повышения спроса на их продукцию при условии неизменности технологий производства, полное потребление воды в этих отраслях возрастет согласно коэффициентам, указанным в следующей таблице.

• Полное потребление воды в 2002 г., млн.куб.м

• 

• У угольной промышленности, промышленности строительных материалов, легкой промышленности сравнительное небольшое прямое потребление , что может привести к недооценке влияния этих отраслей на ОС, если не учитывать косвенное потребление этих отраслей.

• Результаты можно использовать как инструменты хозяйственного планирования с учетом воздействия на ОС, как в масштабах национальной экономики, так и на региональном уровне путем анализа изменений в структуре производства при изменениях в потреблении воды и наоборот.

• Экспорт воды из России

• Вода- особый и уникальный природный ресурс, возобновимый, но незаменимый.

• Россия по водообеспеченности на душу населения занимает в мире второе место после Бразилии.

• Ученые России в последнее время рассматривают водные ресурсы России как серьезную альтернативу невозобновимым ресурсам на мировом рынке.

• «Экологический рюкзак»

• Для полной оценки всех затрат воды при производстве водоемкой продукции на экспорт необходимо учитывать и ее косвенные затраты, чтобы в полной мере оценивать соответствующий «экологический рюкзак», совершенствовать технологии производства и вовремя принимать меры, способствующие снижению затрат воды на вех этапах производства.

• Экологический рюкзак

• «Экологический Рюкзак» оценивает потребление природных ресурсов таким образом, что вычисляется средний вес природных ресурсов, затраченных на услуги и производство. Например, тонна минералов необходима, чтобы произвести 5-граммовое золотое кольцо, и эту цифру надо удвоить, если добавится преобразованная величина энергии и потребления химикатов на единицу продукции. Подобным образом зубная щетка потянет полтора килограмма, если рассмотреть целиком ее экологическое воздействие.

• На основе данных об экспорте основной продукции отраслей минерально-сырьевого комплекса России( Система таблиц «Затраты-выпуск» России за 2002 год, 2005) были получены данные по экспорту воды из России, а именно, полным затратам этого ресурса на производство продукции на экспорт.

• Здесь учитываются полные затраты воды на производство конечной экспортируемой продукции отраслей.

• Выбор отраслей минерально-сырьевого комплекса был не случаен, поскольку здесь экспортируемая продукция подвергается наименьшему пределу (см. таблицу).

• Экспорт воды из России с основной продукцией отраслей в 2002г., тыс.т

• В рассматриваемых отраслях наблюдается значительное косвенное потребление воды, что находит свое отражение в «экологической рюкзаке» экспортируемой за рубеж продукции, что представлено на следующем рисунке.

• В заключение

• можно сказать, что модель межотраслевого баланса можно применять также при анализе эффективности природоохранных мероприятий, прогнозах воздействия экономической системы на ОС на региональном и глобальном уровнях, оценке экологического ущерба.