Характеристики скорости изменения случайных процессов во времени

Любой случайной процесс можно разбить на гармоники.

Представим процесс в виде суммы четырех гармоник:

Данные сигналы имеют различные спектральные составляющие.

Корреляционная функция

Есть система с двумя входами и одним выходом

- корреляционная функция

Выходная переменная y(t) имеет диапазон отклонений СКО:

Часть дисперсии выходной переменной определяется изменением входных величин х₁, х₂, … х_n. Количественной оценкой связей является отклонение R².

Рассмотрим интервал ( , ), то есть те точки, которые попадают в данный интервал, то есть точки от предыдущих значений данного случайного процесса, то есть можно построить функцию связи: .

Корреляционная функция показывает степень связи текущего параметра с его предыдущим значением.

– максимальное время возможности прогнозировать случайный процесс.

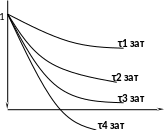
Пример. Предположим показания погоды на текущее время 10⁰⁰ совпадает с показаниями с 9⁰⁰ – 10⁰⁰, но менее совпадают с показаниями с 7⁰⁰ и еще более расходятся с показаниями вчерашнего дня, прошедшей недели и т.д. То есть, корреляционная функция R_xx(0)=1 при τ=0 постоянно падает до нуля при τ>τ_зат. Вид корреляционной функции и время затухания являются количественными характеристиками случайного процесса.

Белый шум, цветные сигналы

Белый шум – сигнал, случайный процесс которого не прогнозируется ни на какое время τ. Белый шум – чисто случайный процесс.

По мере вырезания высокочастотных гармоник, появляется возможность прогнозировать случайный процесс на 1 – 2 шага. Прогнозируемый сигнал называется стохастическим. Характеристикой белого шума является дисперсия.

Спектральная плотность

Спектральная плотность показывает разложение дисперсии по частоте, то есть случайный процесс можно разложить на гармоники.

X₁(t) → ω₁, σ_x1², (S_x1); ω=2πf₁

X₂(t) → ω₂, σ_x2², (S_x2)

X₃(t) → ω₃, σ_x3², (S_x3)

На компьютере всегда можно разложить случайный процесс на составляющие, определить их частоты и дисперсии. Покажем график спектральной плотности:

Площадь под кривой спектральной плотности равна сумме дисперсий гармоник и соответственно равна дисперсии исходного случайного процесса.

Оказывается, что спектральная плотность является преобразованием Фурье от автокорреляционной функции случайного процесса:

По уравнению Эйлера

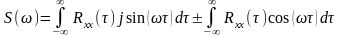
Постановка задачи построения математической модели (идентификация)

Объект управления принято изображать структурной схемой:

х – вектор входных контролируемых факторов Х=(х₁, х₂, … х_n),

Е=(е₁, е₂, … е_n) – вектор входных неконтролируемых факторов,

У=(у₁, y₂, …y_n) – вектор выходных параметров.

Пусть реальный объект описывается уравнениями: Y=F₀(x, E), так как вектор Е не изменяется, то модель процесса строиться в виде: Ŷ=F(x).

Ŷ означает прогнозируемое по модели значение выходного фактора.

Обратим внимание, что структурная схема исходного уравнения и модели различны, то есть нельзя построить полностью достоверную модель. Задача заключается в нахождении зависимости F→F₀, так как структура разная близость оценивается по их реакции на одно и то же входное воздействие.