9.1. Выбор оптимальных решений в условиях полной информационной неопределенности

Вся хозяйственная практика в любой стране — это прежде всего огромное число постоянно принимаемых решений, направленных на реализацию главной цели — достижение производственного и коммерческого успеха.

Хозяйственные решения во всем своем многообразии выделяют­ся по иерархическому уровню (отрасль, объединение, производство и т. п.), по продолжительности осуществления (на сутки, т. е. еже­дневно, на месяц и т. п.), по степени значимости (в зависимости от уровня финансирования и других условий), по характеру действий, отвечающих содержанию решения, и по другим признакам.

Любые решения, направленные на выполнение хозяйственной задачи, предполагают привлечение к делу финансовых средств, ма­териальных ценностей, информации и иных ресурсов. Руководи­тель, менеджер прослеживает результаты принимаемых решений. Они могут быть более или менее удачными или вовсе ошибочными. Последствия решений связаны с тем, какое влияние или воздейст­вие, или противодействие на них может оказывать другая „сторо­на", с которой так или иначе связана реализация ресурсов и других производственных операций. Отсюда очевидно, что производствен­ный и коммерческий механизм рынка обусловлен взаимодействием двух субъектов — двух игроков. Опыт позволяет каждому из них делать надлежащие выводы и выбирать лучшее решение. Такого рода игра требует оптимального решения, обеспечивающего опти­мальный успех.

Взаимодействие двух игроков, ориентированное на взаимный и долговременный успех каждого, называется стратегической иг­рой. Каждый из игроков полагается на лучший исход своих реше­ний в хозяйственной или иной практике, осуществляемой на „игро­вом поле".

В дальнейшем будем рассматривать лишь общую модель страте­гии каждого игрока, не обращаясь к специфике его деятельности.

В простейшем виде стратегическая игра есть игра с нулевой суммой: один из игроков выигрывает столько же, сколько проиг­рывает другой. Действия игроков А и В не носят случайного харак­тера, результат их зависит от выбранной стратегии. Условия игры задаются матрицей выигрышей (а₀), которая имеет вид:

Действия		Действия dj игрока В
d, игрока .4	d,(B)	d2{B)	d,(B) ... dml(B)
dx(A)	au	«12	a13 ... alm
d2(A)	«21	a22	a23 ••• 0.2m
d3(A)	«31	a32	a33 ■■• a3m
d„(A)	a„i	an2	an3 ••• anm

Элементы a_j; матрицы (а,_у) выражают суммы, которые обязан уплатить один игрок другому в соответствии с установленными „правилами игры". Они „предписывают" каждому игроку свою стратегию: для игрока А — выбор одной из строк i, а для игрока В — одного из столбцов /. Исход игры определяется величиной a_tj как пересечение i-й строки и j-го столбца. Игровое поле, согласно матрице выигрышей, может содержать „свою" область выигрыша для данного игрока, не известную партнеру. Пусть игрок А выбрал стратегию d₂{A), а игрок В — стратегию й_л(В). Эта ситуация харак­теризует выигрыш игрока В, который составил а₂₃. Однако воз­можна и другая характеристика игрового поля. Выбор той или иной стратегии связан с распознаванием поведения другого игрока. Стратегическая игра осуществляется в условиях полной информа­ционной неопределенности. Это один из вариантов выбора реше­ния, которое к тому же называется статистическим в условиях их возможного множества.

В реальных условиях руководитель („игрок") располагает ста­тистическими сведениями о результатах своих действий (решений) и о том, на какие действия партнера они были рассчитаны. Это осуществляется на игровом поле с двумя действующими субъек­тами. Тем самым может быть выстроена матрица выигрышей кон­кретного игрока. Например, необходимо установить, выбрать эко­номически приемлемого поставщика продукции или товара для данного производства. Выбор поставщика и есть хозяйственное стратегическое решение, которое предполагает действия — его реа­лизацию. Любое решение, направленное на выполнение хозяйст­венной или коммерческой задачи, требует привлечения к делу оп­ределенного рода ресурсов. Это могут быть финансовые ресурсы (деньги), материальные ресурсы (техника, технология, продукция, продукты), дополнительно привлекаются ресурсы времени и труда.

Однако возможна иная ситуация прохождения игры. С одной стороны, руководитель (субъект), с другой — условие, влияющее на осуществление действия (решения). Таким внешним фактором чаще всего выступает состояние природы, в частности погодные или климатические условия. В этом случае особая роль может отво­диться погодо-климатическим ресурсам, а сами решения будут уже погодо-хозяйственными.

Выбор оптимального решения предполагает, что игроку извест­ны пороговые условия стратегической игры или так называемые правила выбора решения.

9.1.1. Метод минимакса—максимина

Игровая матрица выигрышей, ее называют еще платежной мат­рицей, отражает как возможные выигрыши, так и проигрыши. Ес­ли игрок А выигрывает, то, естественно, игрок В проигрывает. Одновременно не может быть ни того ни другого состояния для иг­роков А к В. Зная свои максимальные проигрыши, игрок В будет руководствоваться принципом, который указывает на необходи­мость ограничить риск больших потерь. В условиях полной неопре­деленности относительно возможных проявлений природы (погоды, климата и др.) для этой цели используется принцип „минимакса", предложенный А. Вальдом. Оптимальное стратегическое поведение (dj = d_onT) сводится к выбору такой стратегии, которая обеспечивает минимальный проигрыш из максимально возможных. Метод ми­нимакса — это достаточно разумный подход, когда один из игроков полностью не осведомлен об особенностях поведения второго. Принципиальное положение метода иллюстрируется в табл. 9.1.

Игрок А в свою очередь может выбрать иной подход — ориенти­роваться на „максимальный выигрыш из минимально возможных". Это есть метод максимина. Такой подход также обеспечивает выбор

А

оптимальной стратегии di = d_onT.

Таблица 9.1 Матрица выигрышей л Стратегия игрока A, di	Стратегия игрока В, d,			Возможный минимальный выигрыш игрока Л
	в,	Вг	в3
А,	8	12	20	8
А2	12	10	21	10
А3	30	25	17	17
Возможный макси­	30	25	20	А —>макс 17 (максимин)
мальный проигрыш				В —» мин 20 (минимакс)
игрока В

В зависимости от оценки результатов принимаемых решений (стратегий) как игрок А, так и игрок В могут выбрать любой из приведенных методов выбора стратегии.

Рассмотрим далее особую ситуацию, довольно распространен­ную, когда в качестве „противника" (партнера) игрока А выступает природа. Она не обладает свойством преднамеренных действий и ее ожидаемое поведение характеризуется полной неопределенностью (без привлечения дополнительной информации).

Множество хозяйственных и коммерческих задач требует учета состояний природной среды. Это могут быть как погодные, так и климатические условия. Например, задачи по транспортировке грузов: выбор сезона, маршрута, вида транспорта или иного вида деятельности. Возможно строительство коммерческого объекта, что также требует знаний, скажем, микроклиматических условий и выбора такой стратегии поведения, которая обеспечивает минимум издержек строительства или максимум выгоды (доходов) в процессе реализации этого объекта.

Выбранная дискретность природных условий, в том числе и по­годных, показывает возможное число стратегий для игрока- субъекта. Число стратегий (решений) может задать сам игрок (ру­ководитель, менеджер и т. п.) на основании выбора мероприятий, которые могут принести различный экономический результат.

Игра — ориентация на возможное состояние погоды — постоян­но контролируется. Ее результаты представляются в виде матрицы полезности (ац), элементы которой а_(у могут выражать затраты (издержки, убытки) или выгоды в зависимости от производствен­ной (или иной) специфики игрока и „способности" погоды вредить или благотворить^. Участие в „игре" такого игрока А, как природа (погода, климат), характеризуется тем, что его „стратегия", „дейст-

Л

вия" di выступают уже как проявление отдельных фаз, состояний, условий и т. п. — Ф,, которые не известны игроку В. Остается неиз­вестной частота осуществления состояний погоды или климата. Фазы, градации состояний природных условий могут задаваться игроком В (руководителем, менеджером), а значения элементов a_tj — возможных затрат или выгод — результат обстоятельных, взвешенных расчетов, отражающих последствия выбранных дейст­вий dj и последующих фаз, градаций Ф,. Вид такой матрицы полез­ности (а,₇) дан в табл. 9.2.

¹ В июле 2001 г. в Читинской области в районе пос. Гусиное Озеро от удара мол­нии загорелся военный склад с боеприпасами. Взрывы снарядов и ракет вызвали пожар огромной силы. Однако через двое суток сильные ливневые дожди полностью погасили страшный пожар

Поведение игрока А — приро­ды (погоды, климата) Ф;	Стратегия, решение, действие d} игрока В
	d,	d2	d3	d.1	d,5
Ф, Фг Ф3 Ф4 макс j амин 1 1 Примерная матрица поле мальные погодо-хозяйственны пояснения метода „минимакса-	3 7 6 2 5 7 2 :зности npi е решения —максими	5 И 3 1ведена из ' (1999 г.) -т".	5 8 3 8 3 работы JI. Там же д	4 6 ш А. Хандо» аны допол	4 4 4 6 4 6 3 .ко „Опти- нительные

Рассмотрим ситуацию, когда элементы матрицы полезности от­ражают затраты, которые могут быть в случае стратегий d_x - d_s. В соответствии с теорией стратегической игры для выбора оптималь­ного решения, действия используется метод (принцип) минимак- са. Для каждого решения d, устанавливается максимальное значе­ние издержек а, (от i = 1 до i = п — 5) (см. табл. 9.2). Таким образом по всем возможным стратегиям (решениям) d_} будут выбраны зна­чения

а™*⁰ = макс a{dj, Ф,) (i = 1, п; j = const).

i

В наборе максимальных значений а""", приходящихся на d_jt

выбирается минимальный элемент, который соответствует опти­мальному действию dj = d_onT и определяет выбор оптимальной стра­тегии согласно минимаксу:

«мин =^{мин макс} «Ц,Ф,). (9.2)

' t

Согласно данным табл. 9.2, оптимальной будет стратегия d₂ = d_lmT.

Таким образом будет определяться поведение руководителя (иг­рока В) как наиболее допустимое с позиции минимизации затрат, издержек. Риск максимально возможных потерь будет ограничен. Принцип минимакса отражает осторожный выбор стратегии игро­ком В с природой А. Тем самым достигаются лучшие результаты в наихудших ситуациях, что проявляется в условиях полной неопределенности относительно осуществления Ф,-.

Рассмотрим далее ситуацию, когда элементы матрицы полезно­сти а,у отражают доходы, которые могут быть получены при реали­зации стратегий dj - d_b. Для каждой возможной стратегии d_} опре­деляется минимальное значение дохода а, в соответствии с методом (принципом ) максимина

^а"и" ^{= мин} > ^ф/) (i = 1> ^п\ i = const).

Из всех минимальных значений ct,""", отвечающих стратегиям

(решениям) d_jy определяется максимальное. Тем самым устанавли­вается оптимальная стратегия (оптимальное решение) dj = d_onT ру­ководителя (игрока В) в условиях полной неопределенности отно­сительно осуществления Ф,

«макс = ^{макс МИН a}(^di> ^Ф1 )• (9.3)

I I

Согласно данным табл. 9.2, оптимальной будет стратегия d₄ = d_m„.

Минимаксный подход в выборе оптимальной стратегии может быть использован в проблеме решения метеоролого-экономических задач, требующих знания климатологической информации. Дейст­вительно, в этих случаях построение матрицы расходов невозмож­но осуществить методом экспериментирования. Требуется задание определенных типов погоды или климатических условий Ф, и соот­ветствующих им необходимых издержек.

К таким задачам можно отнести:

• выбор объемов сезонного запаса топлива;

• выбор оросительной системы и нормы орошения в зависимо­сти от влагообеспеченности;

• выбор места строительства объекта (коммунального, торгово­го или иного назначения) в зависимости от комплекса мезо- и мик­роклиматических условий;

• выбор урожайного сорта сельскохозяйственной культуры в зависимости от водопотребления в заданных районах и многие дру­гие задачи.

9.1.2. Метод Гурвича

В ситуациях, для которых характерны и выгоды, и издержки, что типично в повседневной хозяйственной практике, возможно компромиссное решение. Определяется среднее значение по мини­муму (а_М1Ш) и максимуму (а_макс) при известных решениях-стратегиях dj. Такой метод (принцип) допускает компромиссный взвешенный подход к наибольшей и наименьшей возможностям, которые отве­чают экономическим последствиям принимаемых решений. Пола­гая одинаковыми „веса" последствий, результатов стратегий, реше­ний, принцип Гурвича допускает осреднение: а = 0,5(a_M1I11 +а_МШ{С). Оптимальной принимается промежуточная стратегия. В табл. 9.2 она будет соответствовать d₃.

9.1.3. Метод Сэвиджа

При разработке и решении некоторых метеоролого-экономи- ческих задач более содержательно использовать не сами значения потерь, издержек или доходов (a_f>), а разности a,_v или a*_jy отра­жающие меру снижения полезности, если принимаемая стратегия или решение dj не оптимальны относительно выбранного фактора

Матрицу полезности, представленную элементами а,, в табл. 9.2, можно преобразовать. Устанавливаются последствия ошибочных решений путем сопоставления результатов a_tj возможных страте­гий, которые были по заданному состоянию погоды (климата) Ф,.

Выделяют два вида последствий принимаемых стратегий, ре­шений.

1. Пусть элементы матрицы полезности (см. табл. 9.2) пред­ставляют собой расходы, потери. Тогда можно установить, на­сколько они превышают минимальные при данной фазе Ф₍, т. е. оп­ределить величину

a_Lj - a_jy - мин a_vr (9.4)

Элементы новой матрицы выражают превышение потерь. Мат­рицу такого рода называют матрицей опасений (табл. 9.3).

Выбираются максимальные опасения a_tj при данной стратегии

dj. Оптимальная стратегия d_om устанавливается по принципу ми­нимакса²⁶

^do_m = «ми= ^{мин макс} V (9-5)

it

Таблица 9.3 Матрица опасений. Значения аг =а;. - мин а;. Фазы погоды, климата, Ф,	Стратегия (решение), dj
	d,		d2				da	d4
		0			2		0	1	1
Ф2		4			0		2	1	1
Фз		2			0		4	1	0
		0			1		2	3	4
ф5		2			1		0	3	1
макс а.ц		4			2		4	3	4

Расчеты показывают (см. табл. 9.3), что в этом случае d_onT = d₂.

2. Будем теперь полагать, что а_у (см. табл. 9.2) суть выгода. То­гда можно определить значения a_ijy характеризующие потерю вы­годы или ее снижение относительно максимальной выгоды при данной фазе погоды (климата) Ф_;:

а* = макс а_ц - а_ц. (9.6)

Согласно данным табл. 9.2, при фазе Ф₁ и (a_i;)_MaKC = 5 находим ряд a-j : 2; 0; 2; 1; 1. В итоге матрица последствий ошибочных ре­шений, или матрица сожалений, будет иметь вид, представленный в табл. 9.4.

Таблица 9.4 Матрица сожалений. Значения а;* = макс at- - atj Состояния погоды, климата, Ф,	Стратегия (решение), dj
	d1		d2		d3				d.,
Фх		2		0			2				1	1
ф2		0		4			2				3	3
Ф3		2		4			0				3	4
ф4		4		3			2				1	0
Фь		1		2			3				0	2
макс Яу		4		4			3				3	4

Выбор оптимальной стратегии, решения d_t = d*_onT отвечает усло­вию — принципу минимакса

«С = a_MH„(dj) = мин макс а*. (9.7)

j I

Выбираем решение d_r при котором значение макс а*. минималь­но. В этом суть правильного выбора. В приведенном фрагменте хозяй­ственной практики мин макс a'j = 3. Это указывает на два возможных

оптимальных решения: d*_nT =d_g=d_ll. Такой исход оценки потребует от руководителя окончательного стратегического решения.

Значения а,, и а₍* Е. Е. Жуковский называет метеорологиче­скими потерями, а Н. А. Багров — приведенными.

9.1.4. Метод Хоменюка

Для выбора оптимальной стратегии, решения используется принцип потенциального распределения вероятностей. Он состоит в том, что допускается влияние природной среды в виде суммы вкла­дов отдельных ее состояний в формирование минимальных расхо­дов или максимальных доходов.

Л

(9.8)

Потенциальное распределение вероятностей возможных потерь p_i устанавливается как долевое выражение суммы потерь при осуществ­лении Ф). В методе Хоменюка допускается рассматривать потенциаль­ный вектор Pi=(Pi) как вероятность состояния среды = р(Ф,). Ес­ли элементы матрицы полезности a_tj представляют собой потери, из­держки, тогда искомые вероятности находятся по формуле

1Л

^Г1 п т

Е2Л

i=i/=i

По сведениям, приведенным в табл. 9.2, определяются значения р, (табл. 9.5).

ф,	«У							Kv i	A Pi
	d,	d2	d3
ф,	3	5	3		4		4	19	0,173
Ф-г	7	3	5		4		4	23	0,200
Ф3	6	4	8		5		4	27	0,245
Ф,	2	3	4		5		6	20	0,182
Ф5	5	4	3		6		4	22	0,200
		II"» i i						111	1,000

Выбор оптимальной стратегии dj = d_onT осуществляется на осно­вании критерия Байеса

^а(А^о„т) = ^минЕР₍^а(Ц)- (9-9)

I i

Суммы Y,Pi^ai(dj) определяются в соответствии с распределени-

i

ем a_tj:

Хр, a_i(d₁)= 0,173 • 3 + 0,2 • 7 + 0,245 • 6 + 0,182 • 2 + 0,2 • 5 = 4,75

i

Хр, a,(d_t) =

i

Xp,a,(d₃) = 4,81

i

XPi ^ai(d._t) = 4,83

i

XPi^ai(^ds) = ⁴>¹⁶-

(

Оптимальной, согласно (9.9), можно считать стратегию d₂ = d_onT. Если считать, что в матрице полезности элементы a_tj суть доходы, то потери полезности можно установить в виде снижения доходов

л

макс а, - а, и их вероятности p_t при осуществлении фазы Ф,:

i

т

Х(макс a_tj -a,j) ■ (9.10)

^г * п т ⁴ '

Ц(макс а--а_ц) /=1;=1

3,79

Воспользуемся данными, приведенными в табл. 9.4. Итоговые результаты представлены в табл. 9.6.

Потенциальное распределение вероятностей потерь полезности ф,	^(максау -ац) i	Pi
ф,	6	0,12
ф2	13	0,26
Фз	13	0,26
	10	0,20
ф5	8	0,16
I	50	1,00

Для выбора оптимальной стратегии (решения) используется по аналогии с (9.9) критерий Байеса в виде

^аСр> ^опт) = ^мин Z Pi(^{макс а}Ч - ^аЧЩ)■ (9-11)

1 i

5

Следуя формуле (9.11), рассмотрим значения под знаком суммы для заданных df.

dj (ij d₂ d₃ d₄ d

X(макс a„ -a_tj) 1,72 3,00 1,64 1Д0 1,48

Метод Хоменюка позволяет считать, что оптимальной стратегией при анализе снижения доходов (макс a_Lj - a,₇) является стратегия d₄.

9.2. Выбор оптимальных решений в условиях частичной информационной неопределенностиВсе хозяйственные решения, а стратегические в особенности, обусловлены внешними (рыночными или иными) постоянно сопут­ствующими факторами. Они достаточно сложны и выступают как второй игрок, действия которого непредсказуемы. Отсюда, как уже отмечалось, первый игрок — лицо, принимающее решение (ЛПР), ищет решение в условиях полной неопределенности. Однако воз­можны такие внешние условия, которые могут быть частично из­вестны. ЛПР может располагать некоторой информацией, частично раскрывающей действия противоположного партнера в „стратеги­ческой игре". В качестве второго игрока, об этом уже говорилось,

рассматривается природа — погодные или климатические условия. Этот „игрок" не имеет намерений выиграть, но обладает своим соб­ственным свойством поведения, которое доступно изучению и в определенной степени распознаваемо.

Будем идентифицировать погодо-климатические условия в ка­честве второго „партнера-игрока".

Рассмотренную ранее минимаксную стратегию называют еще стратегией перестраховщиков. Это оправданное поведение, позво­ляющее избегать серьезных экономических последствий ошибоч­ных решений и действий. Если в качестве второго „партнера- игрока" выступает природа, то ситуацию полной информационной неопределенности можно избежать, если известны вероятности осуществления тех или иных климатических условий, типов пого­ды или ее отдельных фаз.

9.2.1. Метод Байеса—Лапласа

Первоначально Байесом в 1763 г. было предложено в такого ро­да задачах использовать равновероятностные состояния природы. Однако тогда уже такой подход представлялся упрощенным, хотя и позволял при известной матрице полезности дать приближенную оценку ожиданий результативности принимаемых решений.

По заданной дискретности фаз погоды (см., например, табл. 9.2) и известным вероятностям их осуществления (р_;=1//г) определя­ется среднее значение полезности (потерь, выгод) при решении dj

M{a) = £a_ip(n)_i. (9.12)

i=i

В частности, в случае d₁ (см. табл. 9.2) реализуется следующее значение математического ожидания (среднего в статистическом смысле):

M(a)d₁ = 0,2(23) = 4,6.

Остальные стратегии получают следующие результаты: M(a)d₂ = 3,8; M(a)d₃ = 4,6; M(a)d₄ = 4,8; M(a)d₅ = 4,2.

Если значениям а придать смысл потерь, то, очевидно, наиболее выгодным, оптимальным будет стратегическое решение d_onT = d₂. В случае если а отражают выгоду, то экономически оправданной бу­дет стратегия d_om = d₄.

В действительности выбранные фазы Ф, климатических условий имеют разную природную (климатическую) вероятность р, (аналогия проявлений „игрока" А). Тогда формулу (9.12) можно переписать так:

M(a) = ±a_tPl. (9.13)

i=l

Известные мероприятия в мелиорации могут быть показатель­ным примером. Необходимо выдать такую стратегию развития ме­лиорации в регионе, которая выгодно отвечала бы одной из следую­щих климатических характеристик: в засушливые годы р(Ф,) = 0,01; в годы со слабым увлажнением р(Ф₂) = 0,15; в годы с умеренным увлажнением р(Ф₃) = 0,55; в годы со значительным увлажнением Р(Ф\) ⁼ 0,20; в годы с избыточным увлажнением р(Ф_ъ) = 0,09.

По формуле (9.8) определяются средние издержки, основанные на вероятностной оценке климатических условий. Согласно табл. 9.2, находим:

M(a)d_x = 5,23; M(a)d₂ = 3,66; M(a)d₃= 6,25; M(a)d₄= 4,93;

M(a)d₅= 4,25.

Оптимальной следует рассматривать стратегию, которая обеспе­чивается действием d_om - d₂.

9.2.2. Метод Байеса

Кроме приведенного выше используется иной, более эффектив­ный подход. Смысл его состоит в следующем. Руководитель пред­приятия, диспетчерской службы, проекта, службы материально- технического обеспечения, поставки ресурсов и т. п., одним сло­вом, лицо, принимающее хозяйственное решение d_jt вырабатывает стратегию поведения с учетом ожидаемых погодных или климати­ческих условий. Будем в дальнейшем называть ЛПР потребителем метеорологической информации, или просто потребителем (см. п. 2.1). Утверждается, что выбор им наилучшей оптимальной страте­гии &>₀„_Т из возможных стратегий & основан на том условии, что из­вестны результаты совместных осуществлений решений d_t и фактической погоды Ф, или определенных условий климата.

Каждый потребитель располагает достаточно объективной ин­формацией о своей зависимости от погоды. Она прежде всего вы­ражается в том, что решения (действия) потребителя d_jt ориентиро­ванные на погоду Ф„ будут сопровождаться экономическим резуль­татом, условно называемым полезностью (а,-), которая может быть

выражена в виде выгоды или потерь. Различные сочетания d_l ~ Ф, образуют матрицу полезности как дискретное выражение некото­рой функции полезности а = а(Ф, d). Матрица полезности имеет стоимостное выражение.

Типичной является ситуация, когда потребитель принимает решение в соответствии с ожидаемой погодой П_}. При этом потреби­тель будет выбирать такой метод разработки прогнозов, который наилучшим образом отвечает выполнению его хозяйственной зада­чи. Большинство потребителей в различных отраслях производства используют в основном методические прогнозы, разрабатываемые в прогностических подразделениях Росгидромета. Эти прогнозы рас­сматриваются как официальные.

Однако такого рода метеорологические прогнозы могут разраба­тываться несколькими, включая коммерческие, прогностическими учреждениями (в пункте, в районе), имеющими лицензии Росги­дромета. Потребитель может выбрать более предпочтительную, бо­лее выгодную прогностическую информацию.

Кроме того, наряду с метеорологическими прогнозами имеется возможность выбора иных прогнозов, разработка которых не требует физического обоснования. Это могут быть инерционные прогнозы, в основе которых лежит исходная погода, или прогнозы по местным признакам и другие подходы, вплоть до случайных прогнозов.

Методические и неметодические прогнозы обобщаются в виде матриц сопряженности, что позволяет установить повторяемость (допускаем интерпретацию вероятности) осуществления отдельных фаз погоды ри = р(Ф„ ITj).

Итак, потребитель располагает экономической информацией о возможных последствиях своего поведения и метеорологической,

Совместные (р,₇) и условные (q_it) вероятности позволяют перейти

к оценке средних потерь R, которые может нести потребитель при стратегическом выборе ориентации на те или иные прогнозы:

которая представляется рядом матриц сопряженности ||ra_l7|| прогно­зов, разрабатываемых на основании некоторых методов. Обобщение этих прогнозов можно представить следующим образом:

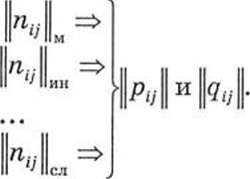
Л = д[а(Ф, d), р(Ф, П)\

Если потребитель постоянно доверяет тем или иным прогнозам, то число его действий d-_r отвечающих содержанию прогноза, будет соответствовать числу текстов прогнозов П_г Следовательно, обе матрицы ||а_гу|| и |p_j;.| будут иметь одинаковый размер п (строк) х

х т (столбцов).

Механизм выбора оптимальной стратегии в рамках байесовско­го подхода состоит в апробации известных потребителю методов прогнозирования по степени обоснования и выбора таких прогно­зов, которые обеспечивают ему или минимум потерь (мин R), или

максимум выгоды (макс G). Тем самым устанавливается опреде­ленный экстремум

S>(a) = extra. (9.15)

s>

Этим достигается условие выбора оптимальной стратегии

R ОПТ = мин R

(Щ

(9.16)

или

GonT = макс G.

(9.14)

ИГлава 10

ОСНОВЫ ВЫБОРА ОПТИМАЛЬНЫХ ПОГОДО-ХОЗЯЙСТВЕННЫХ РЕШЕНИЙ