8.2. Априорные и апостериорные вероятности

Задачи, решаемые в экономической метеорологии, требуют зна­ния вероятностных характеристик осуществления фактических и прогностических метеорологических величин и явлений погоды. Их вероятностная природа рассматривается как случайное проявление любого состояния среды. Здесь необходимо отвлечься от физической природы этих состояний и понимать их как отдельно взятые призна­ки, события, которые наблюдаются случайно, т.е. возникают в силу стечения обстоятельств. При таком подходе дается вероятностная оценка любого события как отдельно взятого в наборе событий.

Как в метеорологической среде, так и в целом в гидрометеороло­гической в качестве такого случайного события рассматриваются все явления (грозы, шквалы, туманы, гололед, ветровые или па­водковые наводнения, ураганный ветер и др.), а также фиксиро­ванные значения метеорологических величин (температуры, ветра, поля давления и др.).

Кроме вероятностного описания метеорологических условий в некоторых задачах используются вероятности осуществления „со­бытий", относящихся непосредственно к области производства (реализация объемов сбыта данной продукции; нарушения в техно­логическом режиме, нестабильность транспортных потоков, потери по метеорологическим причинам и др.).

Теория вероятностей изучает такие случайные события, кото­рые отвечают случайности их проявления и для которых возможна объективная оценка любой доли из всех случаев. При этом допуска­ется осуществление необходимого комплекса условий:

• события проявляются в одинаковых условиях (природных, производственных и иных);

• обозначенные в ряду этих условий события независимы,

• события считаются равновозможными;

• события обладают статистической устойчивостью (устойчи­вость частот относительно среднего от выборки к выборке).

Следует заметить, что необходимые условия носят гипотетиче­ский характер и в реальных вариациях состояний природной среды не всегда полностью выполнимы. Здесь более сложные случайные проявления, чем это очевидно из тривиального примера о выпа­дающем числе очков на верхней грани игральной кости.

Классическое определение вероятности события А, т. е. р(А), ос­новано на понятии элементарных событий А, равновозможных и в равной мере однородных. Иначе

p(A) = n/N, (8.7)

где п — число элементарных событий данной однородности или типа А; N — общее число событий, содержащее А, наряду с другими событиями иной однородности.

Вероятность, как видим, события А проявляется через поведе­ние его частоты. Если условия, сопутствующие событию А, прояв­ляются N раз, а само событие осуществляется п раз, то при боль­ших N частота n/N оказывается близкой к р(А) (закон больших чи­сел).

Если число событий стремится к бесконечности, то вероятность р(А) выступает уже в качестве вероятностной меры на множестве событий или на пространстве £"2, содержащем А.

В реальных оценках вероятность р устанавливается на основа­нии конечного числа N, обеспечивающего требования достоверно­сти статистической выборки.

Вероятность случайного события измеряется числом, заклю­ченным между 0 и 1. Если событие при данном комплексе условий невозможно, его вероятность равна 0. При вероятности, равной 1, событие называется достоверным.

Рассмотрим два природных равновозможных события: дождь (Ф) и отсутствие дождя (Ф). За определенный период времени подготов­

лена статистически представительная выборка N, позволяющая ус­тановить вероятности каждой из выбранных фаз дождя р(Ф) и р(Ф):

(8.8)

и

(8.9)

Прежде всего для определения вероятностей р(Ф) и р(Ф) выби­рается ряд эмпирических данных. Эмпирические данные — это свод статистических сведений как результат последовательной, не­прерывной выборки исследуемого признака, действия, состояния и т.п. Поэтому полученные вероятности являются эмпирическими.

Поскольку вероятности наличия (Ф) или отсутствия (Ф) дождя отражают характерные черты погодных условий (в данном пункте, районе) за длительный период, они рассматриваются как показа­тели климата и называются климатическими вероятностями. Климатические вероятности могут быть установлены и для других явлений и условий погоды. Важным условием является сбор стати­стически надежного объема информации.

Если рассматривать полученные вероятности р(Ф) и р(Ф) с пози­ции теории вероятностей, то можно утверждать, что выбранные фазы дождя дополнительно ничем не обусловлены, кроме как „действиями" самой природы. Такие вероятности называются еще и безусловными.

При относительно малых числах N отношению n/N приписывают термин повторяемость. Использование термина вероятность в этих

Рю

0,5

1985

1990 1993

0 I—i 1981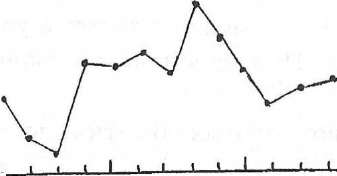

случаях может оказаться недос­таточно обоснованным, хотя и приемлемым для приближенной оценки. Например, может быть установлена повторяемость гроз в Санкт-Петербурге (рис. 8.1) за каждый год. В свою очередь по­вторяемость за период наблюде­ний (1981—1993 гг.) может уже рассматриваться как величина, близкая к вероятности р₁₀ гроз в Санкт-Петербурге.

Рис. 8.1. Повторяемость р₁₀ гроз в Санкт-Петербурге

.Вероятности р(А), отражающие природные или иные события, определяются независимо от лица, выполняющего эти операции, т.е. являются результатом объективной оценки, а потому называются априорными вероятностями (известными до „опыта", независимы­ми от „опыта"). Вероятности р(Ф) и р{Ф) являются априорными. В табл. 8.2 приведен пример априорных вероятностей скорости ветра для различных дискретных значений, используемых на практике.

Таблица 8.2 Априорная мера (вероятность) градаций скорости ветра Ф; М/С	п(Ф,)	Р(Ф<)	П(Ф)	р(ф)	п(Ф)			Р(Ф,)
Ф,(0—5) Ф2(6—11)	158 446	0,158 0,446	|б04	0,604		■820	0,820
Ф3(12—14) Ф4(15—19)	216 98	0,216 0,098	|з14	0,314
Ф5(20—24) Ф6(> 25)	68 14	0,068 0,014	|82	0,82		•180	0,180
I 1	1000	1,000	1000	1,000	1000			1,00

Рассмотрим теперь, что некоторое условие погоды не только осуществляется (Ф) как реальность природы, но и прогнозируется (П). Пусть в прогнозе допускается только одна из двух фаз условия погоды: „ожидается", „не ожидается"; „возможно", „не возможно". Обобщение таких прогнозов приведено в матрице сопряженности IJj ~ Ф, (табл. 8.3).

Таблица 8.3 Матрица сопряженности альтернативных прогнозов Фактически наблюдалась погода, Ф,	Прогноз IIj			Ё«; м
	П — неблаго­приятная пого­да ожидается	П — неблагоприятная погода не ожида­ется (ожидается благоприятная погода)
Ф	пп	«12	«10
Ф	П21	«22	«20
П I«< i=i	«01	«02	N

Выбранное явление или некоторое состояние как случайное со­бытие подвергается статистическому анализу безотносительно к физической природе явления или условия погоды.

Будем полагать, что N — общее число случаев — отражает большую статистическую выборку. Тогда частоты п_м, n_0j и п_и (см. табл. 8.3) можно представить в вероятностной форме.

Безусловные (априорные) вероятности определяются следую­щим образом:

• вероятность неблагоприятного условия погоды (Ф)

р{Ф) = ^, (8-10)

N

• вероятность благоприятных условий погоды (Ф)

р(ф)= lbs. = 1-Иж. (8.11)

N N

Следуя правилу сложения вероятностей, запишем

р(ф) + р(ф) = 1.

Вероятности текстов прогнозов находятся по тем же правилам:

• вероятность текста прогноза — явление ожидается (77)

р(Л)=Al, (8.12)

N

• вероятность текста прогноза — явление не ожидается (77)

Р(Я) = ^-. (8.13)

Сумма вероятностей р(П) и р(П) равна

р(Я) + р(Я) = 1.

Частоты Пц, характеризующие частость сопряжения Л, - Ф₍, по­зволяют установить вероятность осуществления двух совместных событий П и Ф. Такие вероятности называются совместными и выражаются отношением вида

р(П> Ф) (8-14)

N

Информация, представленная формулой (8.14), есть набор пред­сказателей относительно явления Ф. Выбор предикторов Пу осуще­ствлен в рамках метода прогнозирования, и можно полагать, что они содержат информацию относительно явления Ф,. Известно, что совместная вероятность осуществления событий П и Ф равна про­изведению вероятности осуществления П и условной вероятности осуществления Ф при известном П, т. е.

р(П, Ф) = р(П) ■ р{Ф/П), (8.15)

где р(Ф/П) — вероятность осуществления явления Ф, если для предвидения его уже использована дополнительная информация в виде прогноза П.

В силу того что вероятности р(П, Ф) устанавливаются на осно­вании проведенного „опыта" — разработки прогноза или приобре­тения иной дополнительной информации, они получили название апостериорных.

Априорные и апостериорные вероятности приведены в табл. 8.4 (пример).

Таблица 8.4 Априорные (безусловные) и апостериорные (совместные) вероятности Фактиче­ски было, Ф,	Сопряженность вы­ражают частоты n,j					Сопряженность выражают вероятности р(П, ф) - n,,/N
	Прогноз rij			i-i /-1		Прогноз Яу			т
	Я	Я	Я			Я
Ф	16	2	18		р(П, Ф) = 0,16		р(Я, Ф) = 0,02	р(Ф) = 0,18
Ф	3	79	81		р(Я, Ф)=0,03		р(Я,Ф) = 0,79	р(Я) = 0,82
in, f.i	19	81	100		р(Щ = 0,19		р(Я) = 0,81	1,00

8.3. Условные вероятности

По завершении „опыта", т. е. набора данных в виде статистиче­ски значимого ансамбля N изучаемых величин П и Ф, можно уста­новить вероятность иного рода. Сформулируем следующий вопрос: с какой вероятностью можно ожидать явление (условие погоды и т. п.) Ф, если об этом явлении уже имеется предварительная ин­формация в виде прогноза П. Чтобы ответить на этот вопрос, необ­ходимо рассмотреть ряд вероятностных условий.

Допустим, известны априорные вероятности осуществления каждой из двух фаз прогноза скорости ветра: р(Ф) при V > 12 м/с и р(Ф) при V = 0—11 м/с (табл. 8.5).

Таблица 8.5 Матрица сопряженности методических прогнозов скорости ветра при FmT2: 12 м/с. Санкт-Петербург, 1987—1990 гг. ф,	л,		I j
	ri(V > 12)	П (V < 12)
Ф(У> 12) Ф(У< 12) I Примечани рода матриц: „ма прогнозов и факт! рида сопряженное	245 103 348 е. В научной литерат грида сопряженности 1ческих состояний..." ти прогнозов...".	51 815 866 уре встречаются р для прогноза...", и др. Мы будем	296 918 1214 азличные названия такого „матрица сопряженности 1спользовать термин „мат-

По данным табл. 8.5 находим р(Ф) = n₁₀/N = 296/1214 = 0,244 и р(Ф)= n₂₀/N = 918/1214 = 0,756. Эти вероятности могут быть ин­терпретированы как природные (климатические), полученные в результате обработки данных наблюдений за скоростью ветра в Санкт-Петербурге за четырехлетний период в холодную часть года.

Допустим альтернативу (Ф, Ф) и рассмотрим два предиктора (П, П) — предсказатели той или иной фазы скорости ветра.

В реальной синоптической практике прогноз скорости ветра яв­ляется многофазовым. Число прогнозируемых градаций достаточно велико. Однако здесь рассматривается простая альтернатива в силу того, что на сегодня условия использования прогнозов в основном сложились именно в виде такой же альтернативы. Например, при V = 0-^11 м/с регламентируются рабочие, производственные условия, а в случае F_mT > 12 м/с производство функционирует в режиме „за­щиты". На основании матрицы сопряженности (см. табл. 8.5) можно установить вероятность осуществления текстов прогнозов Л и Л.Так,

П_ Ф

(8.16)

Р(П) = 1Р(Ф₁)Р

Л,

;

Ф

\ ■ у

П

i о

где =

Пусть всего составлено 1214 прогнозов. Из 296 случаев Ф на

признак П пришлось 245, т.е. р

1 = 0,828.

£ | = 0,112.

{Ф

Ф

В свою очередь этому признаку П соответствовало 103 из 918

случаев Ф, что составляет р

Отсюда полная вероятность признака 77 определяется так

:

р{П) = р(Ф)Р

(8.16')

£ +р(Ф)р|

или р(Л) = 0,244 • 0,828 + 0,756 ■ 0,112 = 0,287.

Действительно, р(П) = = 348 :1214 = 0,287.

N

Вероятности р(Ф) и р(Ф) выполняют роль весовых коэффициен­тов при относительных долях (0,828 и 0,112) осуществления текста П в реализациях Ф и Ф.

В свою очередь полная вероятность противоположного признак

а

77 Ф

, равная 0,713.

+ р(Ф)р

Ф

П есть величина р(П) = р(Ф)р

Суммарная вероятность признаков (77, 77): ]Гр(77_у) = 1.

1

Теперь поставим задачу несколько иначе. Требуется найти ус­ловную вероятность того, что заданному тексту 77 принадлежит фа­за Ф или что этому же тексту 77 — иная фаза Ф. Тогда можно вос­пользоваться формуло

й

fф ^

(8.17)

П

1 = 1,2 п.

Возможна противоположная постановка задачи и поиск услов­ной вероятности иного характера, а именно

'П⁴

(8.18)

Ф

Р(Я,Ф,)

Из уравнений (8.17) и (8.18) следуют оценки совместных веро­ятностей р(П, Ф) и р(Ф, П), что позволяет перейти к равенству

'п⁴

р{ф,)р

ф

V ' у

р(П)р\

п

Отсюда с учетом (8.16) и принадлежности Ф₁ к условию у нахо­дим условную вероятность осуществления фазы Ф, при известном тексте прогноза Л

р(ф,)р

ф

(8.19)

п

71

Ф

v

I Р(Ф,)Р

i=1

Уравнение (8.19) называют формулой Байеса, или формулой ве­роятностей гипотез Ф_г.

Вместо уравнения (8.19) представляется возможным использо­вать более простое выражени

е

П_

Р(Ф,)Р

Ф

(8.20)

\ ' У

р(П

)

Формула (8.19), как и (8.20), отражает условную вероятность появления, осуществления некоторого признака (явления, небла­гоприятного или благоприятного условия погоды ит. п.) Ф, при из­вестном условии (тексте прогноза) П. В этом и содержится ответ на вопрос, поставленный в начале п. 8.3.

В соответствии с формулой (8.20) апостериорная оценка, в част­ности совместная вероятность р(Ф, П), пропорциональна произве­дению априорной оценки р(Ф) на правдоподобие полученной ин

­

П_

Ф

формации р

насколько вероятно получить информацию П, если полагать, что явление Ф осуществилось. В свою очередь частное от деления двух

*ж

р(П)

вероятностей

Величина -^^рассматривается как мера того, есть отношение правдоподобия для правиль­

ного прогноза Ф. Согласно данным табл. 8.5,

'Я'

= 2,88.

Ф

₌ 245 . 348 ₌ 0,827

р(Я) ~ 296 ' 1214 ~ 0,287

Выражая формулу (8.19) или (8.20) через частоты п,₇ альтерна­тивного прогноза (см. табл. 8.3), запише

м^пю я„ N п,_п

Ф

м)

(8.21)

= ?п

"4)1

N

'01

— условная вероятность успешного прогноза наличия явления;

_ "21 _

= 921

(8.22)

"01

— условная вероятность ошибочного прогноза наличия явления;

(8.23)

(8.24)

(8.25)

условная вероятность ошибочного прогноза отсутствия явления;

^П22 = ~ = Я₂2

— условная вероятность успешного прогноза отсутствия явления. В итоге матрица условных вероятностей р(Ф,/Л_;) = q_tj выглядит

так:

/	п	п
ф	Чи	Я12
ф	Я 21	<?22
1 К i	1	1 )

Если использовать те же данные табл. 8.5, то априорная (при­родная) вероятность фазы V > 12 м/с р(Ф) будет равна 0,244. Ис­пользование метода прогнозирования скорости ветра позволяет увеличить вероятность осуществления этой градации до значения

Гф)

pi —1 = 0,704. Условные вероятности, как видим, больше безуслов­ных.

(фЛ

Следует подчеркнуть, что условные вероятности q_tj = р —- ,

i У

определяемые по формуле Байеса, дают полное описание в вероят­ностной форме достоинств той или иной прогностической информа­ции, которая используется потребителем в оперативной хозяйст­венной практике.

Поскольку условные вероятности (8.21)—(8.24) установлены после проведения „опыта" — использование предиктора П, то такие вероятности называются еще апостериорными условными вероят­ностями.

На основании данных табл. 8.5 находим значения д,₇(табл. 8.6).

Таблица 8.6 Условные вероятности qtj осуществления Ф; при известном тексте прогноза /7( Фактически было, Ф,	Прогноз [Jj
	П			П
Ф	Яи= nu/noi= 0,704		?12= nl2/nQ2= 0,059
Ф	?21= "2l/"oi= 0,296		q22=n22/n02 = 0,941
П (=i	1,000		1,000

Отсюда следует, что в целях получения более достоверных све­дений о явлении Ф (любом природном состоянии) используется до­полнительное условие или в виде прогноза П, или в виде иной ин­формации, в той или иной мере связанной с условиями осуществле­ния Ф.

Матрицы сопряженности прогнозов (см. табл. 8.4) и условных (см. табл. 8.6) вероятностей разрабатываются по сезонам года или рабочим периодам (навигация, отопительный сезон, период поса­дочных работ в сельскохозяйственных предприятиях и т. п.).Наряду с условными вероятностями q_tj = ^ — рассчиты-

Р(П,)

ваются условные вероятности иного рода — использования текста П при осуществившемся уже явлении Ф.

Другими словами, устанавливается соотношение вида

Яц = , _L , • (8.26)

Р(Ф,)

По формуле (8.26) определяется вероятность правильных про­гнозов наличия явления р(П/Ф)

р(П/Ф) = -^ = д'₁₁. (8.27)

"ю

Величина q'_n является мерой предупрежденности явления Ф. В синоптической практике оценке предупрежденности опасного явления придается особое значение, что непосредственно связано с убытками, которые несет потребитель.Глава 9

ЭЛЕМЕНТЫ ТЕОРИИ СТРАТЕГИЧЕСКИХ ИГР