1.5. Газовые (воздушные) трансформаторы теплоты.

Принципиальные схемы и термодинамические циклы газовых трансформаторов теплоты.

Газовые трансформаторы теплоты чаще всего используют воздух в качестве рабочего тела и поэтому обычно называются воздушными. Они отличается от парокомпрессионных тем, что весь цикл происходит в газовой фазе (т.е. без изменения агрегатного состояния рабочего тела). Вместо дроссельного вентиля используется турбина (детандер), совершающая работу и находящаяся на одном валу с компрессором, что позволяет снизить мощность привода компрессора и обеспечивать более глубокое охлаждение воздуха при расширении по сравнению с адиабатным дросселированием. Принципиальная схема и термодинамический цикл такой машины показаны на рис. 16.

Принцип работы такой машины становится понятен при рассмотрении термодинамических процессов рабочего тела в ТS - диаграмме:

1-2 – адиабатное сжатие в компрессоре - КМ;

2-3 – изобарное охлаждение воздуха в воздухоохладителе – ВО ( отвод теплоты - q₁ от рабочего тела при постоянном давлении);

3-4 – адиабатное расширение воздуха в детандере - Т;

4-1 – изобарный отвод теплоты из холодильной камеры ХК (или подвод теплоты - q₀ к рабочему телу).

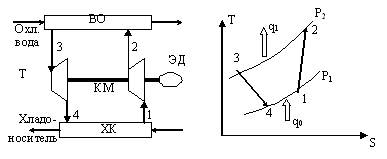
Рис. 16. Схема и термодинамический цикл воздушной холодильной машины.

Процессы сжатия в компрессоре и расширения в детандере происходят с увеличением энтропии вследствие необратимости. Весь цикл заключён между двумя изобарами Р₁ и Р₂.

Холодильная камера – ХК может служить непосредственно холодильником (без промежуточного хладоносителя). В этом случае холодный воздух после расширения в детандере поступает в камеру, охлаждает её и выбрасывается в атмосферу, а в компрессор поступает свежий воздух из атмосферы.

Цикл воздушной холодильной машины в р-v диаграмме изображен на рис.17.

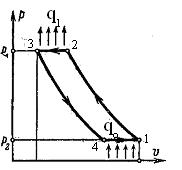
Рис. 17. Термодинамический цикл воздушной холодильной машины в P-V диаграмме.

Холодильный коэффициент воздушной холодильной машины:

или иначе:

.

Но так как:

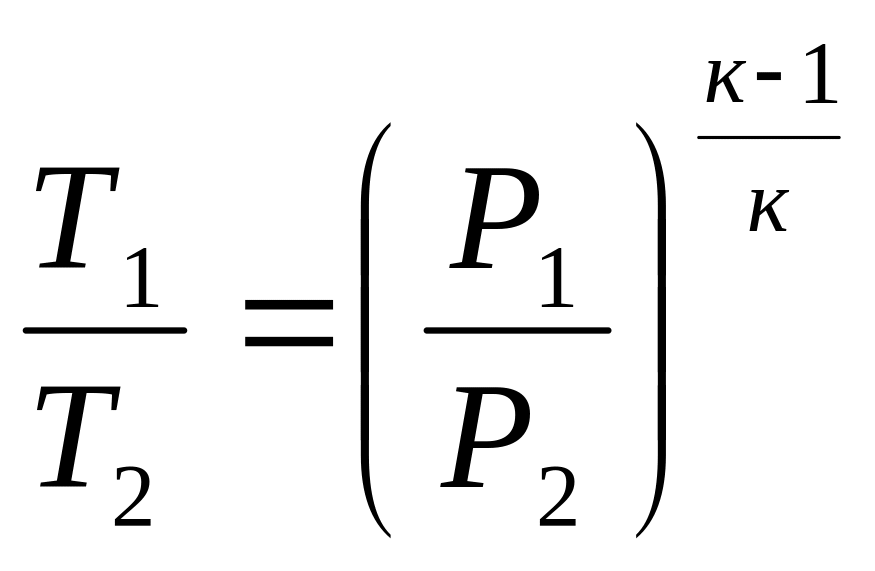, и также ,

то отсюда следует, что:

или (что то же самое):

.

После чего получаем:

.

Это выражение можно представить иначе:

.

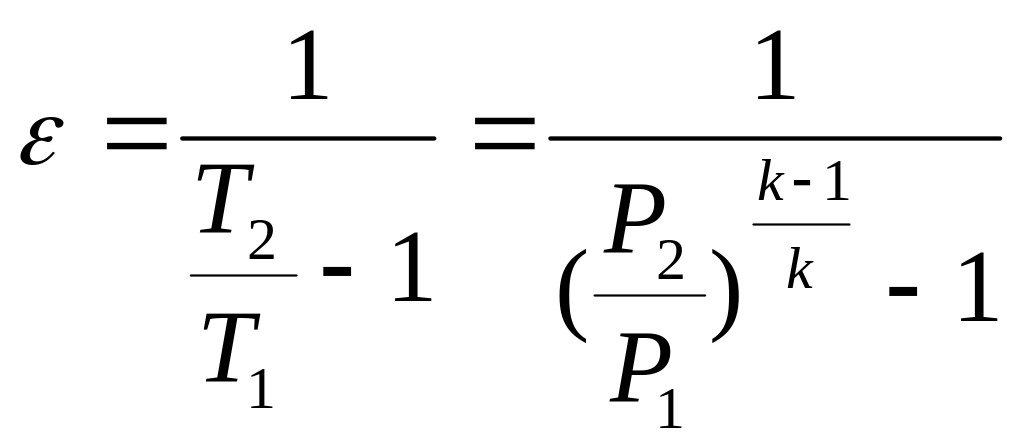Сравнение циклов воздушного трансформатора теплоты и эквивалентного цикла Карно.

Газовые холодильные машины имеют невысокий холодильный коэффициент. Для сравнения на рис.18 показаны обратный цикл Карно и обратимый цикл воздушной холодильной машины, обеспечивающие одинаковые температуры горячего и холодного источников: Т₁ и Т₀.

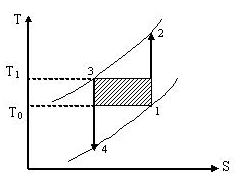
Рис. 18. Сравнение обратных циклов Карно и воздушной холодильной машины

Из рисунка видно, что работа цикла Карно L значительно ниже, а холодопроизводительность  Q₀ больше, чем у воздушной машины. Следовательно холодильный коэффициент цикла Карно значительно выше, т.к.:

Примеры сравнения.

1. Сравним холодильные коэффициенты обратного цикла Карно и воздушной холодильной машины (ВХМ) при следующих условиях:

Р₁=1бар; Р₂=4бара; t₃=+20^oC = 293К. Рассмотрим два варианта:

а) t₁=-20^oC = 253К; ;

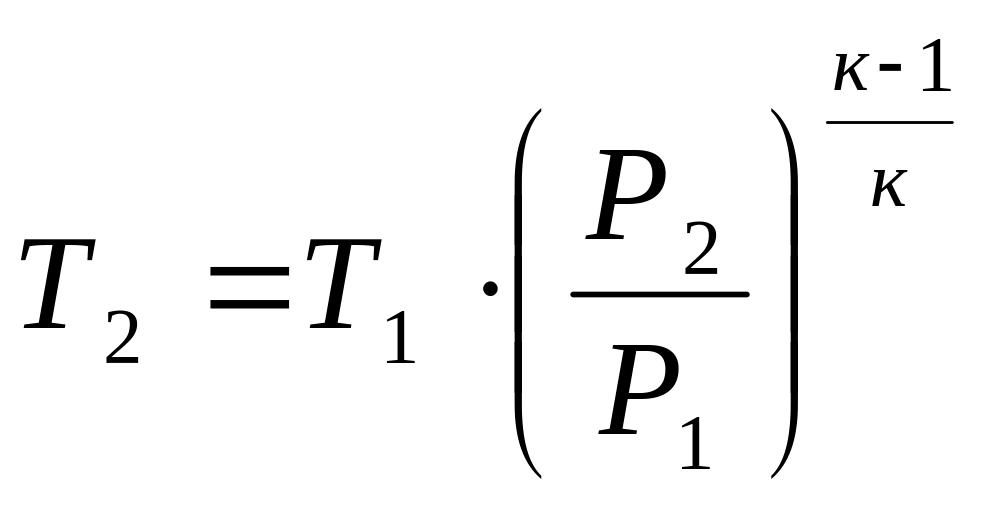Т₂ = 2534^0,4/1,4 =376К. Холодильный коэффициент:

цикла Карно _к = = = 6,3;

ВХМ _ВХМ = = = 2,06.

Т.е. цикл Карно в3 раза эффективнее цикла ВХМ.

б) t₁=-5^oC = 268К;

Т₂ = 2684^0,4/1,4 =398,2К. Холодильный коэффициент:

цикла Карно _к = = = 10,7;

ВХМ _ВХМ = = = 2,06.

Т.е. цикл Карно в5 раз эффективнее цикла ВХМ.

Следует обратить внимание на то, что холодильный коэффициент ВХМ не изменился, т.к. не изменились давления Р₁ и Р₂. А т.к. , то это означает, что отводимая теплота и затраченная работа возрастают одинаково

2. Выполним те же расчёты для газовой холодильной машины с одноатомным газом (например, аргоном) и трёхатомным (например, диоксидом углерода – СО₂). Показатель адиабаты 1 - атомного газа к = 1,67; 3 – атомного газа к = 1,29. В обоих вариантах Р₁=1бар; Р₂=4бара; t₃=+20^oC = 293К.

а) Аргон. t₁=-20^oC = 253К;

Т₂ = 2534^0,67/1,67 =441,2К. Холодильный коэффициент:

ГХМ _ГХМ = = = 1,34.

Т.е. холодильный коэффициент ГХМ с 1 – атомным газом в 1,5 раза ниже, чем у цикла с 2 – атомным газом при одних и тех же параметрах.

б) Диоксид углерода – СО₂. t₁=-20^oC = 253К;

Т₂ = 2534^0,29/1,29 =345,5К. Холодильный коэффициент:

ГХМ _ГХМ = = = 2,73.

Т.е. холодильный коэффициент ГХМ с 3 – атомным газом в 1,3 раза выше, чем у цикла с 2 – атомным газом и в 2 раза выше, чем у цикла с 1 – атомным газом при одних и тех же параметрах.

Холодильный коэффициент цикла Карно тот же: _к = = 6,3;

При использовании таких трансформаторов теплоты в качестве тепловых насосов коэффициент трансформации определяется по формуле (1.8):

.

Подставляя сюда значения Q₁ и L в удельном выражении, получим:

Или иначе:

Но так как:

, и также ,

то отсюда следует, что:

или (что то же самое):

После чего получаем:

.

Это выражение можно представить иначе:

.

Из формул (1.6), (1.7) и (1.8) следует, что:

 =  + 1. .

Для условий примера 1 коэффициенты трансформации ТНУ с идеальными (без потерь) газовыми циклами будут иметь следующие значения:

а) для одноатомных газов (например, аргона)  =1,34+1= 2,34.

б) для двухатомных газов (например, воздуха)  =2,06+1= 3,06.

в) для трёхатомных газов (например, диоксида углерода)  =2,73+1= 3,73.

Однако, в реальных установках всегда присутствуют потери. Фактически затраченная работа значительно выше теоретической:

,

где  - коэффициент полезного действия системы компрессор + турбодетандер.

Пример расчёта реальной воздушной холодильной установки.

Условие задачи.

Рассчитать термодинамический цикл воздушной холодильной установки, холодопроизводительность и холодильный коэффициент при следующих параметрах:

• давление: перед компрессором Р₁ = 1 бар; после компрессора Р₂ = 1 бар;

• температура воздуха: на входе в компрессор t₁ = 10 ^оС; после охладителя воздуха t₁ = 10 ^оС;

• производительность компрессора при параметрах всасывания V = 0.1 м³/с;

• эффективный КПД: компрессора _к = 0,8; турбодетандера _т = 0,8;

• теплоёмкость воздуха С_р = 1 кДж/(кг·К) (принимаем постоянной для простоты расчёта).

Решение.

а) Расчёт идеального цикла.

Температура на нагнетании компрессора:

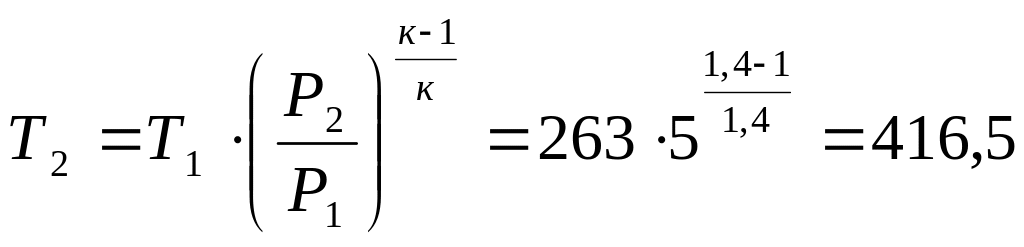К (143,5 ^оС).

Температура на выходе из турбодетандера:

К (94,3 ^оС).

Теоретический холодильный коэффициент:

= = 1,71.

б) Расчёт реального цикла.

Теоретическая работа компрессора:

l_кт = C_p·(T₂ – T₁) = 1·(416.5  263) = 153,5 кДж/кг.

Теоретическая работа турбины:

l_тт = C_p·(T₃ – T₄) = 1·(283  178,7) = 104,3 кДж/кг.

Действительная работа двигателя компрессора:

l_к = l_кт/_к = 153,5/0,8 = 191,2 кДж/кг.

Действительная работа турбины:

l_т = l_тт·_т = 104,3·0,8 = 83,4 кДж/кг.

Фактическая температура на нагнетании компрессора:

T_2д = Т₁ + l_к/ C_p =263 + 191,2/1 = 454,2 К (181,2 ^оС).

Фактическая температура после расширения в турбине:

T_4д = Т₃  l_т/ C_p =283  83,4/1 = 199,6 К (73,5 ^оС).

Плотность воздуха при параметрах всасывания:

= 1,342 кг/м³.

Массовый расход воздуха:

G_в = V_в·₁ = 0,1·1,342 = 0,1342 кг/с.

Мощность привода компрессора:

N = G_в·(l_к  l_т) = 14,5 кВт.

Удельная холодопроизводительность:

q_o = C_p·(T₁ – T_4д) = 1·(263  199,6) = 63,4 кДж/кг.

Удельная теплопроизводительность:

q₁ = C_p·(T_2д – T₃) = 1·(454,2  283) = 171,2 кДж/кг.

Полная холодопроизводительность:

Q_o = q_o ·G_в = 63,4·0,1342= 8,5 кВт.

Полная теплопроизводительность:

Q₁ = q₁ ·G_в = 171,2·0,1342= 23 кВт.

Действительный холодильный коэффициент:

= 8,5/14,5 = 0,59.

Действительный коэффициент трансформации ТНУ:

= 23/14,5 = 1,59.

Аналогичный расчёт для холодильной установки с диоксидом углерода в качестве рабочего тела, у кторого показатель адиабаты к = 1,29; удельная газовая постоянная R = 0.189 кДж/(кг·К); удельная изобарная теплоёмкость C_p = 0,84 кДж/(кг·К) даёт следующие результаты:

Мощность привода компрессора:

N = G_в·(l_к  l_т) = 12,9 кВт.

Полная холодопроизводительность:

Q_o = q_o ·G_в = 8,6 кВт.

Полная теплопроизводительность:

Q₁ = q₁ ·G_в = 21,3 кВт.

Теоретический холодильный коэффициент:

=2,29.

Действительный холодильный коэффициент:

= 0,65.

Действительный коэффициент трансформации ТНУ:

= 1,65.

При этом необходимо отметить, что теоретический холодильный коэффициент уменьшается с ростом степени сжатия компрессора в соответствии с зависимостью: .

А действительный холодильный коэффициент (для принятых выше КПД компрессора и турбины) при степени сжатия выше 2 остаётся практически неизменным. При уменьшении степени сжатия до 1,4 действительный холодильный коэффициент обращается в ноль, что вызвано уменьшением холодопроизводительности в связи с необратимостью процессов сжатия в компрессоре и расширения в турбине.

Термодинамический цикл Джоуля.

Для нагрева воды до более высоких температур с целью ее использования в системах отопления приемлемыми могут оказаться установки, использующие в качестве рабочего тела водяной пар или конденсирующиеся газы (например, диоксид углерода) и работающие по газовому циклу Джоуля (частный случай обобщенного цикла Лоренца). Газовый цикл такой ТНУ показан на рис. 19.

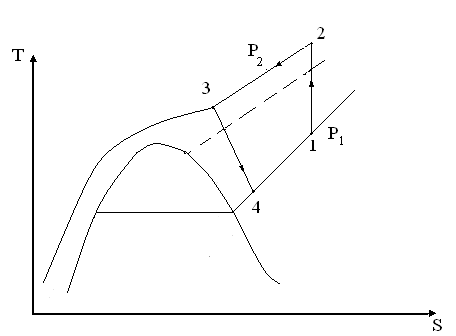
Рис. 19. Термодинамический цикл ТНУ с циклом Джоуля на диоксиде углерода

Температура в т.4 цикла Джоуля определяется расчетом адиабатного процесса расширения рабочего тела в турбине с учетом его необратимости, определяемой заданием внутреннего относительного КПД турбины - _0,i. При этом накладывается дополнительное условие: процесс расширения пара не должен заканчиваться в двухфазной области, т.е. сухость пара в т. 4 не должна быть меньше единицы:

х₄  1.

Эта точка цикла Джоуля определяет температуру охлаждаемой воды НПИТ на выходе из ТНУ. Температура в т. 2 цикла определяется расчетом адиабатного процесса сжатия в компрессоре с учетом его необратимости, определяемой эффективным КПД компрессора:

_е = _i  _м ,

где _i и _m – индикаторный и механический КПД компрессора, соответственно.

Коэффициент трансформации теплоты в таком цикле ТНУ определяется по формуле:

,

где N_к и N_т – мощности компрессора и турбины; Q – теплота, получаемая в нагревателе воды.

Некоторые результаты расчетов приведены в виде графических зависимостей (рис.20) коэффициента трансформации теплоты ТНУ от давления на нагнетании и всасывании компрессора.

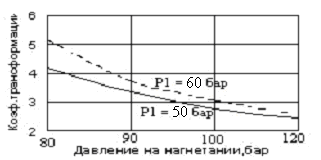
Рис. 20. Зависимость коэффициента трансформации ТНУ с циклом Джоуля от давления на нагнетании компрессора при различных давлениях на всасывании

В расчетах были приняты следующие численные значения некоторых величин:

- эффективный к.п.д. компрессора _е = 0,85;

- внутренний относительный к.п.д. турбины-детандера _оi= 0,85.

При этом мощность компрессора рассчитывается по формуле:

N_к = G(h₂ – h₁),

где G – массовый расход рабочего тела; h₂ и h₁ – энтальпии рабочего тела на нагнетании и всасывании компрессора.

А мощность турбодетандера по формуле:

N_т = G(h₃ – h₄),

где h₃ и h₄ – энтальпии рабочего тела на входе и выходе из турбины.

Энтальпии в процессах теоретического сжатия в компрессоре - h_2T и расширения в турбине - h_4T рассчитываются по уравнению состояния диоксида углерода [2]. Фактические энтальпии с учётом потерь определяются по формулам:

;

.

В упрощённых расчётах можно использовать формулы адиабатного процесса идеального газа.

Мощность компрессора и турбины можно рассчитывать по формулам:

N_к = Gl_к , N_т = Gl_т

где l_к и l_т – действительная удельная работа компрессора и турбины, соответственно:

, ,

а l_КТ и l_ТТ – абсолютные значения теоретической работы компрессора и турбины, соответственно, определяемые по формулам:

;

,

где с_р – средняя теплоемкость газа в соответствующем процессе; R - удельная газовая постоянная; к – показатель адиабаты.

На рис.21 показана зависимость температуры нагреваемой воды на выходе из ТНУ от давления на нагнетании и всасывании компрессора..

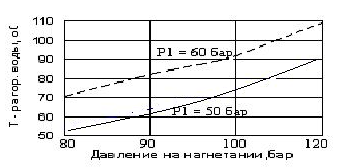
Рис. 21. Зависимость температуры горячей воды на выходе ТНУ с циклом Джоуля от давления на нагнетании компрессора при различных давлениях на всасывании

Эти графики дают наглядное представление о значениях коэффициента трансформации и возможности нагрева воды в ТНУ, предназначенных для целей ГВС и отопления.