
- •1.Основные этапы операцинного исследования.
- •Постановка задачи.
- •Формализация задачи.
- •Нахождение метода решения.
- •Проверка и корректировка модели.
- •Реализация найденного решения на практике
- •2.Типичные классы задач исследования операций (ио).
- •3.Некоторые принципы принятия решений в ио.
- •4.Многокритериальные задачи принятия решений в условиях определенности.
- •5.Методика опр-я полез-ти для ситуации с кач. Крит-ями (р.Акоф, м.Сасиени).
- •6.Принятие решений в условиях риска.
- •7.Принятие решений в усл. Неопр-ти (Крит. Вальда, Лапласа, Гурвица, Сэвиджа).
- •8.Критерии Вальда, Лапласа, Гурвица, Сэвиджа (частный случай)
- •9.Р азвернутая форма игры.
- •10.Нормальная форма игры.
- •11.Ситуации равновесия.
- •12.Игры с нулевой суммой. Антагонистич. Игры. Теорема о ситуациях равновесия.
- •13.Смешанные стратегии. Максиминные и минимаксные стратегии игроков.
- •14.Теорема о минимаксе. Лемма 1 (об опорной гиперплоскости).
- •15.Теорема о минимаксе. Лемма 2 (об альтернативах для матриц).
- •16.Доказательство теоремы о минимаксе.
- •17.Вычисление оптимальных стратегий (поиск решения в чистых стратегиях, доминирование стратегий, решение игр 2x2).
- •18.Решение антагонистических игр методами линейного программирования.
- •19.Решение методами линейного программир-ия матричных игр с ограничениями.
17.Вычисление оптимальных стратегий (поиск решения в чистых стратегиях, доминирование стратегий, решение игр 2x2).
Простейшим является случай, когда
существует седловая точка, т.е. когда
существует элемент
,
являющийся максимальным в своём столбце
и минимальным в своей строке. Тогда
чистые стратегии
и
(или, что равносильно, смешанные стратегии
и
,
для которых
![]() ,
а все остальные компоненты равны нулю)
будут оптимальными стратегиями для
игроков 1 и 2 соответственно.
,
а все остальные компоненты равны нулю)
будут оптимальными стратегиями для
игроков 1 и 2 соответственно.
Доминирование. Пусть дана матрица
.
Будем говорить, что
-ая
строка доминирует
-ую
строку, если
![]() и
и
![]() по крайней мере для одного j.
по крайней мере для одного j.
Аналогично,
-ый
столбец доминирует
![]() -ый
столбец, если
-ый
столбец, если
![]() и
и
![]() х.б. для одного i.
х.б. для одного i.
Т.о., одна чистая стратегия доминирует другую, если выбор первой (доминирующей) стратегии, по крайней мере, не хуже выбора второй (доминируемой) стратегии, а в некоторых случаях и лучше. Отсюда следует, что игрок может обойтись без доминируемых стратегий и использовать только недоминируемые стратегии.
Теорема. Пусть
– матричная игра, и пусть строки
![]() матрицы доминируются. Тогда игрок 1
имеет такую опт. стратегию
,
что
матрицы доминируются. Тогда игрок 1
имеет такую опт. стратегию
,
что
![]() ;
кроме того, любая опт. стратегия для
игры, получ. в результате удаления
доминируемых строк, будет также опт.
стратегией для первоначальной игры.
;
кроме того, любая опт. стратегия для
игры, получ. в результате удаления
доминируемых строк, будет также опт.
стратегией для первоначальной игры.
Аналогичная теорема справедлива и для доминирования столбцов. Общий результат этих теорем состоит в том, что все доминируемые строки и столбцы могут быть отброшены.
Игры (2x2). Пусть
дана матр. игра
![]() с платежной матр.
с платежной матр.
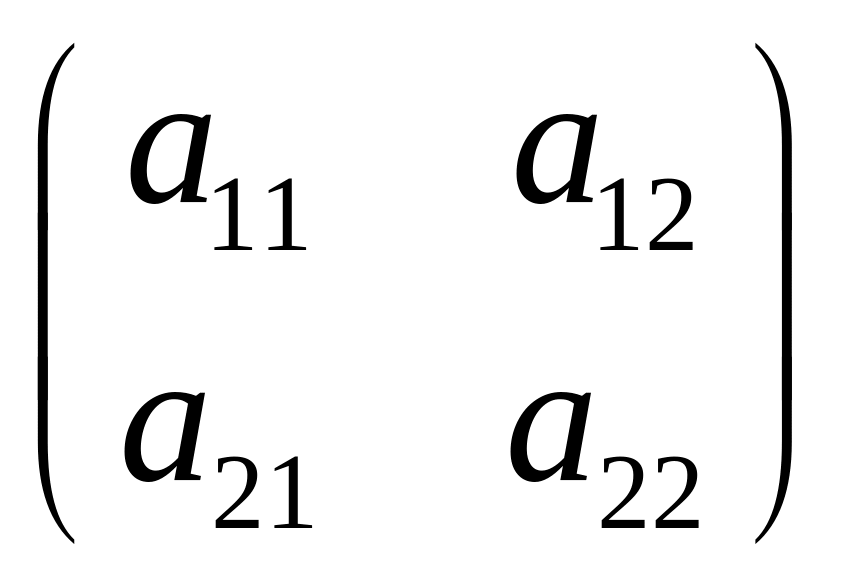 .
Если есть седловая точка, то всё
определено. Если нет, то опт. стр-ии
.
Если есть седловая точка, то всё
определено. Если нет, то опт. стр-ии
![]() и
и
![]() имеют полож. компоненты
,
имеют полож. компоненты
,
![]() .
.
Если значение игры –
,
то для опт. стратегии
,
т.е.
![]() .
.
Преобразуем:
![]() (*)
(*)
Т.к.
оптимальная
стратегия, то должно выполняться:
![]() ,
,
![]() .
.
Допустим, что одно из выражений строго
меньше
:
![]()
Т. к.
![]() ,
,
![]() ,
то левая часть (*) будет меньше правой.
Отсюда следует, что должно быть
,
то левая часть (*) будет меньше правой.
Отсюда следует, что должно быть
![]() ,
,
![]() .
.
Аналогично:
![]() ,
,
![]() .
.
Из этих уравнений, с учётом, что
,
![]() легко найти стратегии обоих игроков.
легко найти стратегии обоих игроков.
18.Решение антагонистических игр методами линейного программирования.
На основании т. о минимаксе, стратегия
,
удовлетворявшая условию
![]() где
– значение игры, является ОС для 1-го
игрока. Т.е. не существует другой
стратегии, которая дала бы ему больший
ожидаемый выигрыш, чем
,
против каждой стратегии игрока 2.
где
– значение игры, является ОС для 1-го
игрока. Т.е. не существует другой
стратегии, которая дала бы ему больший
ожидаемый выигрыш, чем
,
против каждой стратегии игрока 2.
Т.о., игру с точки зрения 1-го игрока можно записать как задачу линейного программирования:
![]() ,
,
![]() ,
,
![]() ;
;
Причём
рассматривается как
![]() -ая
переменная, неограниченная по знаку
(свободная).
-ая
переменная, неограниченная по знаку
(свободная).
С другой стороны с точки зрения 2-го игрока, он стремится минимизировать значение игры:
![]() ;
при
;
при
![]() ,
,
![]() ;
;
;
– своб. переменная |
;
– своб. переменная. |
Т.о., решив одну из двойственных задач, мы определим ОС 1-го и 2-го игроков и значение игры.
19.Решение методами линейного программир-ия матричных игр с ограничениями.
Рассмотрим игру, в которой допускаются не все смешанные стратегии. Обычно для этого имеются определённые практические основания. Предположим, что смешанные стратегии и соответственно должны выбираться из некоторых выпуклых многогранников.
Если матрица игры
![]() ,
то задача игрока 1 состоит в том, чтобы
найти
,
то задача игрока 1 состоит в том, чтобы
найти
![]() (1), где два множества X и Y
определяются соответственно неравенствами
(1), где два множества X и Y
определяются соответственно неравенствами
![]() и
и
![]() .
.
Аналогично задача 1-го игрока состоит
в том, чтобы найти
![]() (2), при тех же ограничениях на
стратегии игроков.
(2), при тех же ограничениях на
стратегии игроков.
В выражении (1) величина в скобках, очевидно, является функцией . Точнее она является значением задачи ЛП, целевая функция которой имеет коэффициенты, зависящие от . По теоремам двойственности, если эта задача допустима и ограничена, то две задачи
 (3) и двойственная к ней
(3) и двойственная к ней
 (4), будут иметь одно и то же значение
целевой функции.
(4), будут иметь одно и то же значение
целевой функции.
Значит, задача игрока 1 сводится просто к задаче максимизации: |
Аналогично, можно показать, что задача (2) игрока 2 сводится к задаче минимизации: |
|
|
Задачи (5) и (6) являются двойственными друг к другу. Если эти задачи допустимы, то выражения (1) и (2) будут равны и, таким образом, игра с ограничениями будет иметь решение в смешанных стратегиях.

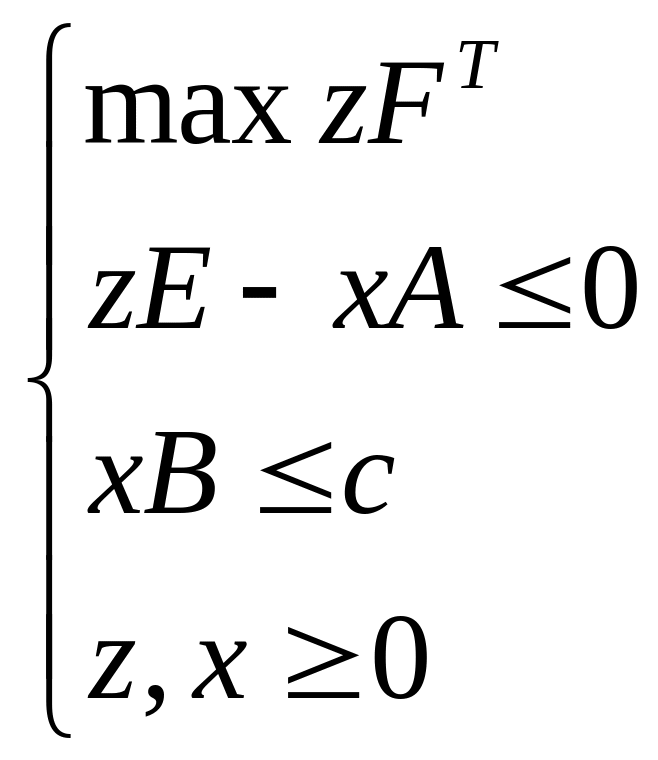 (5)
(5) (6)
(6)