6.Принятие решений в условиях риска.

Такая задача возникает в том случае, когда с каждой принимаемой стратегией связано целое множество различных результатов c известными вероятностями .

Формально модель задачи может быть представлена в виде следующей матрицы:

			…
			…
…	…	…	…	…
			…

Где – П результата при использовании решения .

Пусть заданы усл. вер-ти , , . Тогда , - ожид-ая П каждой страт-ии.

Очевидно, что в кач. оптим-ой стратегии следует выбирать ту, для которой ожидаемая П максимальна.

7.Принятие решений в усл. Неопр-ти (Крит. Вальда, Лапласа, Гурвица, Сэвиджа).

В отл. от задачи принятия реш.-я в усл. риска в данном сл. играет роль и сост-е среды .

Пусть заданы или м.б. опр. П рез-тов при использовании стратегии : .

В завис-ти от сост. среды результат достигается с вероятностью . Набл-лю неизвестно распр-ие вероятностей среды . Относ. сост-я среды набл-тель может только высказывать опред-ые гипотезы. Эти предпол-ия о вероятном сост-ии среды явл-ся субъект-ми вероятностями . Если бы были известны набл-лю, то мы имели бы задачу принятия решения в усл. риска.

1. Критерий Вальда. Это критерий "осторожного набл-ля". Он оптимизирует П в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. По данному критерию решающее правило имеет следующий вид: . По критерию Вальда выбирают стратегию, кот. дает гарантир. выигрыш при наихудшем состоянии среды.

2. Критерий Гурвица. Он основан на след. двух предп-ях: среда может нах-ся в самом невыгодном сост-и с вер-ю , и в самом выгодном - с вер-ю , где - коэфф. доверия. Решающее правило им. вид: , где . Очевидно, что при получаем крит. Вальда, а при 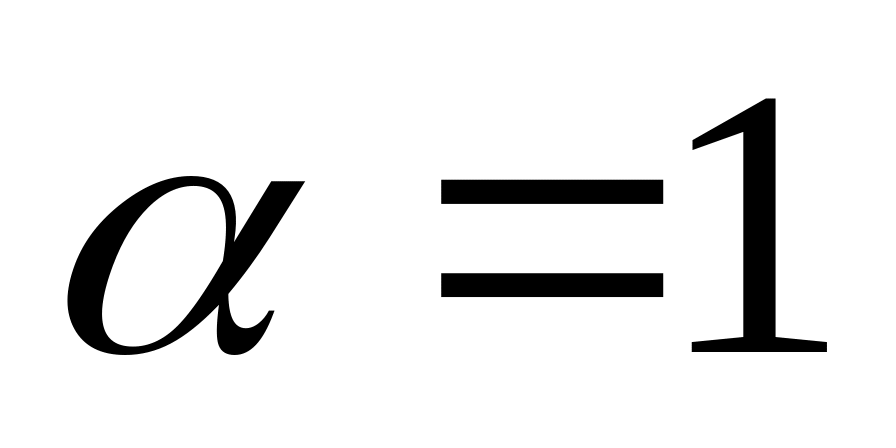- правило , что предст. стратегию "здорового оптимиста".

3. Критерий Лапласа. Если неизвестны вероятности состояний среды, то при данном подходе все сост. среды предпол-ся равновер-ми: . В рез-те решающее правило принимает вид: , при условии .

4. Критерий Сэвиджа. Это критерий минимизации сожалений. "Сожаление" – это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния. Чтобы определить "сожаление", поступаем следующим образом. Строим матрицу , где 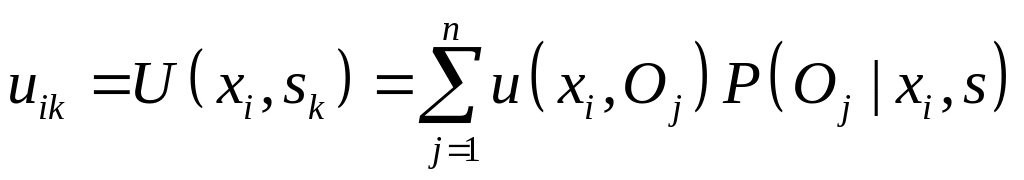, 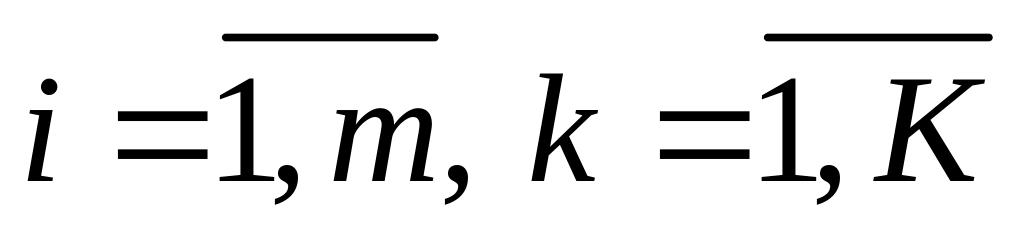. В каждом столбце этой матрицы находим максимальный элемент 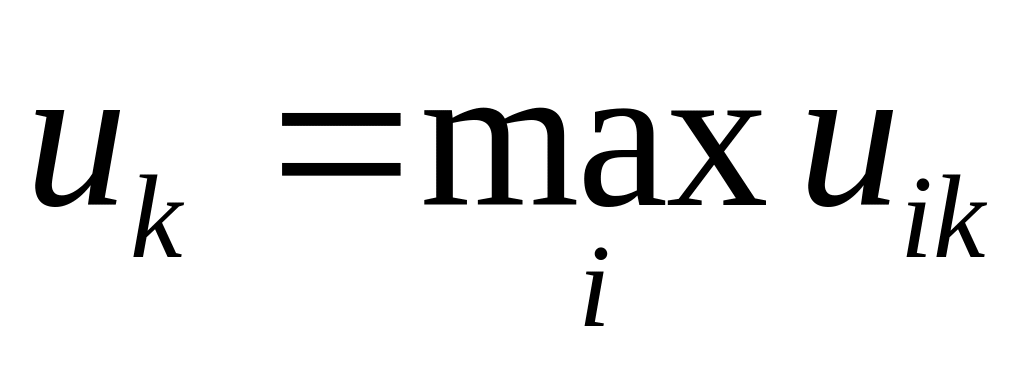. Его вычитают из всех элементов этого столбца, вычисляя величины 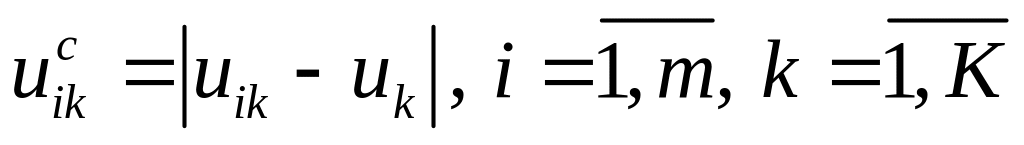, из которых составляют матрицу сожалений 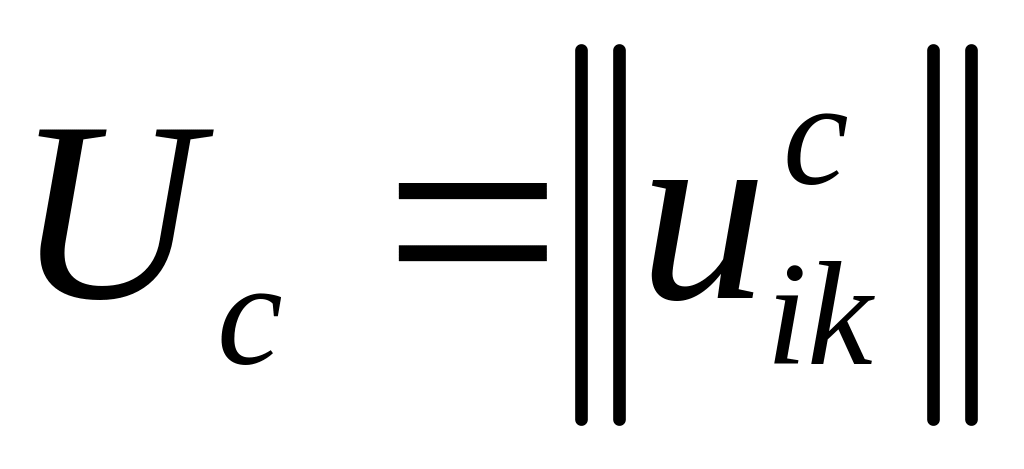. В качестве оптимальной выбирают ту стратегию , которая минимизирует максимальное "сожаление": . Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшим образом отличается от предполагаемого.

8.Критерии Вальда, Лапласа, Гурвица, Сэвиджа (частный случай)

Рассмотрим частный случай модели задачи в условиях неопр-ти. Предположим, что каждому возможному сост-ю среды соотв. один возможный исход: , где при и при . Т.о., в данном случае математическая модель задачи принятия решения определяется множеством стратегий , множеством состояний среды , а также матрицей полезности:

			…
			…
…	…	…	…	…
			…

Где . Множество предполагается неизвестным. В этом случае рассмотренные выше критерии для выбора оптимальной стратегии принимают следующий вид.

1. Критерий Вальда: ,

2. Критерий Гурвица: ,

3. Критерий Лапласа: ,

4. Критерий Сэвиджа: , где .