Одноканальная смо с неограниченной очередью (м/м/1)

Это одна из наиболее часто используемых моделей, относящихся к СМО с ожиданием. При ее рассмотрении принимаются следующие предположения:

- входной поток заявок (требований) - пуассоновский;

- время обслуживании распределено по экспоненциальному закону.

- среднее время обслуживания.

Найти:

- среднее время ожидания

U- среднее время пребывания

- средняя длина очереди

N- среднее количество заявок в системе

- вероятность занятости устройства.

Будем определять характеристики этой СМО по уже рассмотренному в предыдущем случае алгоритму.

1. Введем множество состояний:

S0- канал (система) свободен

S1- одна заявка в СМО или канале и она обслуживается;

S2- две заявки в СМО - одна обслуживается, одна в очереди;

S3- три заявки в СМО – одна обслуживается, две в очереди;

Sn- n заявок в СМО – одна обслуживается, n-1 в очереди.

2.Составим граф состояний и разметим его.

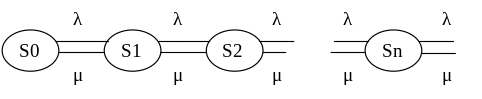
Для этой системы финальные вероятности существуют при , если .

При и очередь возрастает неограниченно.

При система справляется с потоком, если он регулярный.

3. По формулам для процесса гибели и размножения имеем:

; ; ;

Вероятность того, что система пуста:

4. Определим характеристики эффективности

Среднее количество заявок в системе: …

Вероятность занятости системы:

Среднее время ожидания заявок в очереди:

Многоканальная смо с неограниченной очередью (м/м/n)

Для рассмотрения этой СМО снова применим уже использованный нами алгоритм рассмотрения:

1. Зададим множество состояний:

S0 – система пуста;

S1 – один канал занят;

S2 – два канала заняты;

Sn – n каналов заняты;

Sn+k – n каналов заняты, k заявок в очереди..

2. Составим граф состояний и разметим его.

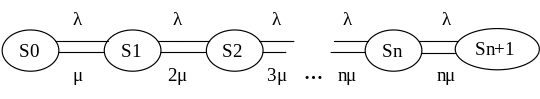
3. По формулам гибели и размножения найдем финальные вероятности.

Финальные вероятности существуют если

…

…

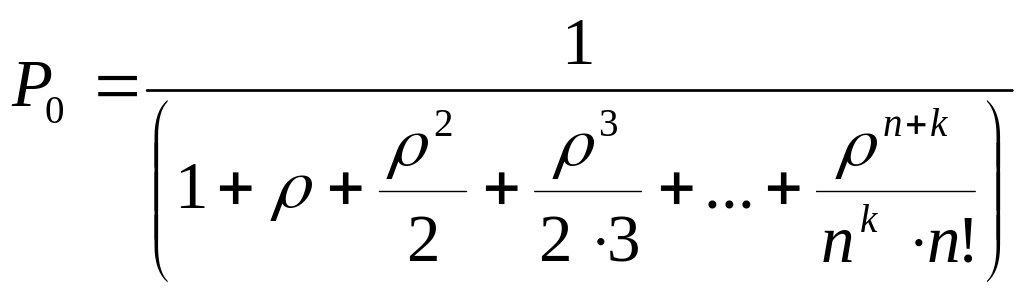
4. Характеристики эффективности.

Среднее число занятых каналов:

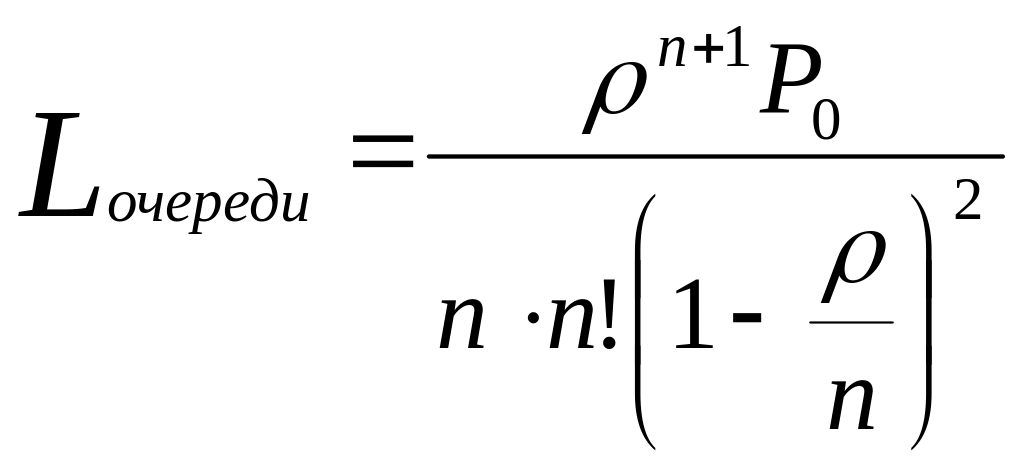
По формуле Литтла:

Пример. В порту имеется два причала для разгрузки грузовых судов. Интенсивность потока судов равна 0,8 судов в сутки. Среднее время разгрузки одного судна составляет 2 сут. Предполагается, что очередь ожидающих разгрузки судов может быть неограниченной длины.

Найти среднее время пребывания судна в порту.

Имеем: m=2, =0,8 сут^-1, , .

Находим:

;

;

.

Итак, сут.

Частным случаем рассмотренной нами системы является СМО, в которой очередь не бесконечна, а имеет конечное значение. Этот случай рассматривается ниже

СМО с ограниченной длиной очереди.

СМО с ограниченной длиной очереди является такая система, в которой требование, поступающее на обслуживание, покидает систему, если заняты все каналы обслуживания, и в накопителе заняты все места.

Вероятности состояний S₀,S₁,…,S_N находят по формуле

, где .

Вероятности состояний определяют с помощью формулы

, где , l – максимальная длина очереди.

Вероятность P₀ подсчитывают по формуле .

В большинстве практических задач должно соблюдаться отношение , тогда выражение для P₀ можно переписать в следующем виде

.

Вероятность отказа в обслуживании определяется из выражения

.

Среднее число каналов, занятых в обслуживании, и коэффициент занятости определяются:

; .

Среднее число свободных аппаратов и коэффициент простоя определяются:

; .

Средняя длина очереди определяется с помощью выражения:

.

Пример. На автозаправочной станции установлены три колонки для выдачи бензина. Около станции находится площадка на три машины для их ожидания в очереди. На станцию прибывает в среднем две машины в минуту. Среднее время заправки одной машины 1мин. Требуется определить вероятность отказа и среднюю длину очереди.

Имеем: N=3, l=3, =2мин^-1, =1мин, . Находим: , , тогда

,

,

.

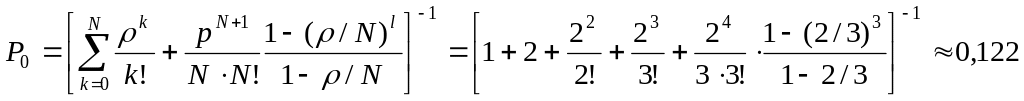Таким образом, , машины.