
- •Определение и сущность эколого-экономической системы (ээс). Принципы устойчивого развития ээс.
- •Принципы устойчивого развития:
- •Принцип Хартвика. Аналитико-теоретическое обоснование измерения экологически отрегулированного («зеленого») внп для невозобновляемых и возобновляемых ресурсов.
- •Сущность и классификация экономико-математических моделей (эмм). Применение эмм в моделировании ээс.
- •Анализ требований к экономико-математическим моделям, описывающим экологически устойчивое экономическое развитие.
- •7. Принципы моделирования экологических процессов и их реализация в модели «хищник-жертва» и модели озерной экосистемы.
- •8. Принципы моделирования эколого-экономического взаимодействия и их реализация в экономико-математической модели оптимального сбора урожая.
- •3.1. Принципы моделирования эколого-экономических систем
- •3.3. Модель оптимального сбора урожая
- •9. Принципы построения имитационных эколого-экономических систем.
- •12. Балансовые эколого-экономические модели оптимизации выпуска продукции и оптимизации дохода. Характеристика основных переменных и структуры, направлений использования.
- •13. Балансовые эколого-экономические модели с увеличением расходов ресурсов и равновесных цен. Характеристика основных переменных и структуры, направлений использования.
- •14. Структура модели моБа с учетом природоохранного фактора в. Леонтьева. Анализ модели с точки зрения соответствия требованиям к моделям, описывающим экологически устойчивое экономическое развитие.
- •17. Модели экономического роста, учитывающие природный капитал. Анализ с точки зрения соответствия требованиям к моделям, описывающим экологически устойчивое экономическое развитие.
- •18. Модель оптимального экономического роста с учетом экологических факторов как задача оптимального управления.
- •20. Система экономических стимулов в управлении качеством окружающей среды и модели обоснования введения платежей за загрязнение окружающей среды в бассейне реки (озера).
- •Модели обоснования введения платежей за загрязнение окружающей среды
- •21. Экономико-математическая модель выбора оптимального режима водопользования предприятием.
- •22. Рыночные методы управления качеством окружающей среды и модель формирования региональной рыночной системы регулирования качества окружающей среды (модели пока нет)
- •23. Моделирование оценки влияния экологических факторов на стоимость имущества и эффективность инвестиций.
- •Методические подходы к учету экологических факторов при оценке эффективности инвестициошшх проектов
- •24. Моделирование оценки влияния развития макроэкономики на окружающую среду. Постановка задачи
- •26 Применение эконометрических моделей для условной оценки качества питьевой воды. – нет!!!
- •27. Методы идентификации экологических рисков в системе экономического управления природопользованием.
- •Методы идентификации рисков
- •Методы статистический идентификации
- •Методы аналитической идентификации
- •Экспертные методы идентификации риска
12. Балансовые эколого-экономические модели оптимизации выпуска продукции и оптимизации дохода. Характеристика основных переменных и структуры, направлений использования.
Пусть F(x1x,2 x n)-целевая функция выпуска, хар-щая пр-во, использующее n ресурсов. Пусть имеется mвидов загрязнения от данного прпоизводства, которые заданы матрицей интенсивности загрязнений
C 11 c 12 c1n
Cр = c 21 c22 c2n
C m1 c m2 cmn
Где с ig>0-колво g-го загрязнения, прдуцируемое при использовании ед-цы i-го рес-са.
Вектор загрязнений определяется по формуле:
‾Z=Cp‾x T или zk=c kj x j (4.18)
Пусть А-матрица к-нтов ограничений на рес-сы, ‾b-вектор ограничений, определяемых возможностями производства.
‾Zдопустимые отходы.
Задача оптимизации выпуска продукции выглядит так:
 F(x
, x , )=F(x)→max
на допустимом множестве (4.19)
F(x
, x , )=F(x)→max
на допустимом множестве (4.19)
‾x>=0, ‾ z>=0
A‾xT<=‾bT (4.20)
‾Z<=‾z*
Приведенная задача оптимизации при условии соблюдения экологических норм соответствует устойчивому инновационно-ориентированному развитию.
Для соблюдения последнего условия в модели, которое можно записать в таком виде
∑c kjx j<=z k*, (4.21)
Необходимо либо делать выбор в сторону более совершенных технологий, либо заменять грязные ресурсы на более чистые.
Модель (4.18)-(4.20) относится к области макроэкономики, когда выпуск можно отождествить с ВВП страны или валовой продукцией региона. Тогда условие (4.21) является управлением технологической политики
Для учета экологического фактора в микроэкономики необходимо перейти к стоимостным выражениям в целевой функции и оплате превышения норм загрязнения.
Пусть р-агрегированная цена производимой продукции, а компоненты вектора
w‾=(w 1, w2, )означают расходы на устранение загрязнений в случае превышения соответствующих норм. Тогда функция дохода от выпуска продукции F(‾x) имеет вид:
P=pF(‾x)- ‾wδ‾, где δ‾- вектор включения санкций оплаты за загрязнения:
 δ
0, zj<=zj*
δ
0, zj<=zj*
1, zj>zj*
‾z-вектор загрязнений,
Zj*-крмпоненты вектора предельно допустимых загрязнений.
Модель оптимизации дохода от выпуска продукции с использованием вектора ресурсов ‾х при технологии, характеризуемой производственной функцией F, определяется следующим образом: найти максимум функции (4.19) на допустимом множестве решений
‾х>=‾0;
A‾x T<=‾bT.
В этой модели присутствуют как возможности самого производства, так и нормативы технологического воздействия на окружающую среду и расходы на ликвидацию последствий их превышения. Видно, что при «жестоком» экологическом законодательстве производитель вынужден будет применять более совершенные технологии с целью снижения удельных техногенных отходов.
13. Балансовые эколого-экономические модели с увеличением расходов ресурсов и равновесных цен. Характеристика основных переменных и структуры, направлений использования.
Для моделирования эколого-экономических систем в макро- и микроэкономике используются и балансовые модели многоотраслевой экономики. В некоторых из них полагается, что необходимо увеличить валовой выпуск с тем, чтобы прирост выпуска направить на устранение или уменьшение загрязнений в окружающей среде. Однако при такой постановке задачи полагается, что используемые технологии остаются на прежнем уровне, что отражено в неизменности матрицы затрат А.
Как правило, матрицы межотраслевого баланса обладают значительным запасом продуктивности. В ряде случаев для минимизации техногенных отходов приходится тратить больше ресурсов на единицу выпуска продукции, т.е. увеличивать внутриотраслевое потребление. Это «утяжеляет» коэффициенты матрицы прямых затрат А, что, в свою очередь, уменьшает запас ее продуктивности.
Вообще говоря, величина элементов аij матрицы прямых затрат А является своеобразным отражением уровня технологий и экономики. Чем меньше аij, тем больше ресурсосбережение и продуктивность матрицы А. Для экстенсивной экономики с затратным технологическим укладом продуктивность матрицы А выдерживается в пределе (число Фробениуса близко к единице). Для развитой экономики с продвинутыми технологиями продуктивность матрицы прямых затрат обладает значительным запасом.
Пусть
А – технологическая матрица межотраслевого
баланса,
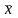 - вектор валовых выпусков отраслей,
- вектор валовых выпусков отраслей,
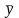 - вектор конечного потребления. Тогда
классическое
уравнение межотраслевого баланса
имеет вид
- вектор конечного потребления. Тогда
классическое
уравнение межотраслевого баланса
имеет вид
=А + . (1)
Предположим, что для проведения экологических и природоохранных мероприятий нужно увеличить внутриотраслевое потребление, т. е. новая матрица прямых затрат представляет собой сумму прежней матрицы А и некоторой добавки. Соответственно изменятся также и векторы валового выпуска и конечного потребления
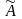 =А
+ ∆А,
*
=
+ ∆
,
*
=
+∆
.
(2)
=А
+ ∆А,
*
=
+ ∆
,
*
=
+∆
.
(2)
Для измененной матрицы уравнение межотраслевого баланса имеет вид
+ ∆ =(А + ∆А)( + ∆ ) + +∆ .
После приведения подобных получаем уравнение для изменения вектора валовых выпусков
(Е - )*∆ =∆А* + ∆ . (3)
Рассмотрим частный случай изменения матрицы А, когда все ее элементы увеличиваются в (1 +α) раз, причем α удовлетворяет условию запаса продуктивности А (матрица (1 + α)А также является продуктивной). Иными словами, ∆А = αA и тогда уравнение (3) с учетом равенства (2) принимает вид
(Е - (1+α) А)∆ =α ( - )+∆ . (4)
Это уравнение связывает изменения валовых выпусков с изменениями расхода ресурсов и вектора конечного потребления. Из него получаем выражение для ∆ :
∆
=(Е
-
(1+α) А)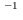 (
α
(
-
)+∆
). (5)
(
α
(
-
)+∆
). (5)
Проанализируем
выражение (5). Так как в силу второго
критерия продуктивности матрицы (1 + α)А
матрица
(Е
- (1
+ α)А)
является положительной,
то даже в случае нулевого прироста
вектора конечного потребления валовый
выпуск продукции увеличивается, поскольку
-
>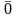 .
.
Пример 1. Найти увеличение валового выпуска для случая двух отраслей с матрицей прямых затрат и неизменным вектором конечного потребления
,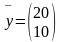
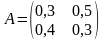
если для соблюдения нормативов загрязняющих отходов необходимо увеличить внутриотраслевое потребление на 10% в каждой отрасли. Решение. Сначала из уравнения (1) рассчитаем исходный вектор валовых выпусков
= (E - A)
Далее, согласно формуле (4), составим все необходимые для вычислений матрицы и векторы:
(1+α)
А = 1,1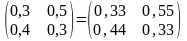 ,
,
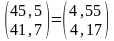
α ( - )=0,1;
(Е
-
(1+α) А)=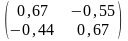 ,
(Е
-
(1+α)А)
=
,
(Е
-
(1+α)А)
=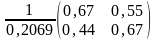 .
.
Наконец, при ∆ = получаем решение уравнения (5)
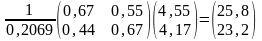
∆ =
Сравнение полученного результата с исходным вектором валового выпуска показывает, что даже при нулевом росте конечного потребления для увеличения внутриотраслевого потребления с целью устранения загрязнений необходимо увеличить валовые выпуски на 39,4 и 44,8% в первой и второй отраслях соответственно. Такой прирост является экстенсивной мерой, которая почти невыполнима в реальных условиях экономики. Более приемлемым в данном случае представляется переход к новым ресурсосберегающим и «чистым» технологиям.
В последнее время урон, причиняемый окружающей среде, обычно компенсируется экологическим налогом и штрафами, что приводит к удорожанию выпускаемой продукции. В этой постановке задачи полагается, что объемы валовых выпусков и внутриотраслевое потребление неизменны, т. е. матрица прямых затрат А не меняется.
Воспользуемся стоимостной моделью равновесных цен. В матричной форме она имеет вид
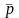 =AT
+
=AT
+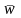 ,
(6)
,
(6)
где и — соответственно вектор цен на продукцию отраслей и вектор добавленной стоимости. Средства, направляемые на устранение загрязнений, увеличат компоненты вектора добавленной стоимости . Пусть вектор ec > — экологическая «нагрузка» в виде налогов, штрафных санкций, расходов на инженерно-профилактические меры и т. д. Тогда вектор цен на продукцию отраслей при затратах на экологию определяется из уравнения
* = (E-AT) ( + ec ) . (7)
Таким образом, изменение цен на продукцию отраслей с учетом составит
∆ = * - = (E-AT) ec. (8)
Поскольку компоненты матрицы (E-AT) в силу продуктивности матрицы затрат А неотрицательны, то ∆ > . Отметим, что в этом случае расход ресурсов на выпуск продукции остается неизменным.
Пример 2. Для трехотраслевой экономики (добыча и переработка углеводородного сырья, производство электроэнергии и машиностроение) определить, как повлияет на увеличение цен продукции отраслей необходимость отчисления на экологические мероприятия 20% от добавленной стоимости в первой отрасли и 15% — в третьей отрасли. Исходные цены по отраслям соответственно равны 20, 15 и 40 ден. ед. Известна матрица коэффициентов прямых затрат
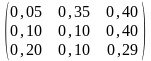
A=
Решение.
Вектор
цен имеет вид
=
(20, 15, 40)T,
тогда из формулы
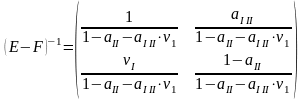 (9)
(9)
вычисляем сначала вектор добавленной стоимости по отраслям:
=
(E-AT)
=
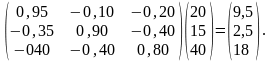
Затем определяем, согласно условию задачи, вектор экологической добавленной стоимости:
ec
=(1,9; 0; 2,7)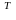 .
.
Далее вычисляем матрицу (Е - АT) -1, и затем уже по формуле (9) определяем приращение ценового вектора, компенсирующее затраты на устранение загрязнений (частичное или полное):
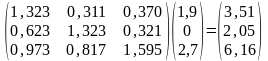
∆ =
Таким образом, в результате указанных отчислений в первой и третьей отраслях цены на продукцию возрастут на 17,6, 13,7 и 15,7% соответственно по отраслям.
Удорожание экологически чистой продукции является уже почти нормой в экономике. Особенно это видно в производстве сельскохозяйственной продукции. Основной причиной этого является использование традиционных технологий, требующих значительных затрат на минимизацию техногенного воздействия на биосферу.
