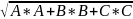26.Квадратичные формы. Матрица квадратичной формы. Канонический вид.

Матрица вида

а11 а12 а1n

а21 а22 а2n

…

аm1 аm2 аmn

назыв. матрицей квадратичной формы. Т.к в матрице аij=aji для всех i, j=1, …, n, то матрицу А назыв. симметрической. Тогда: А^Т=А. Если ׀А׀≠0, то квадратичную форму f (х1, х2, …, хn) назыв. невырожденной, а в противном случае-вырожденной. Пусть квадратная форма f (х1, х2, …, хn) задается матрицей А. Рассм. матрицу Х=(х1, х2, …, хn). Тогда квадратичную форму можно задать в матричном виде: f(х1, х2, …, хn) = X*A*X^T. Пусть f (х1, х2, …, хn)- квадратичная форма. Если в записи формы f все коэф. aij=0 для i≠j, I, j=1,…,n, то в этом случае, говорят, что форма имеет канонический вид: f (х1, х2, …, хn) = a11x²1+a22x²2+…+annx²n. Теорема: Любую квадратичную форму с помощью линейного преобразования можно привести к каноническому виду. Др. словами, заменяя переменные х1, х2, …,хn на новые переменные, получаем канонический вид формы. Способы приведения квадрат. формы к каноническому виду: 1) выделение полных квадратов: f (х1, х2) = =х²1+2х1х2+х²2; последнее сворачивается (х1+х2)². Сделаем замены переменных: у1=х1+х2, у2=х2. Тогда вид такой: f=f(y1;y2)=y²1-канонический вид формы f. Если в записи формы f все коэф. aij=0, где i=1, …, n, то вначале нужно сделать замены переменных: x1=u1-u2, x2=u1+u2, x3=u3,…,xn=un. При этом в записи формы f появятся квадраты переменных, далее можно применять метод выделения полу квадратов. 2) ортогональное отображение: в этом случае квадратичная форма f приводится к след. виду: f (х1, х2, …, хn) = =λ1у²1+λ2у²2+…+λny²n, где λ1, λ2, …, λn - собственные числа линейного отображения с матрицей А. Линейное отображение назыв. ортогональным, если оно сохраняет длины векторов. 3) использование главных угловых миноров матрицы

Среди всех квадрат-х форм выделяют положительно-определенные: квадрат-я форма f (х1, х2, …, хn) назыв. положительно-определенной, если для любого набора переменных х1, х2, …, хn≠Ѳ справедливо: f (х1, х2, …, хn)>0.

27.Критерий Сильвестра положительной определённости квадратичной формы.

Теорема: Квадратичная форма явл. положительно-определенной, когда все главные угловые миноры матрицы квадратичной формы положительны. Пусть f(х1, х2, …, хn) и g(y1, y2,…,yn)- две кватрат-е формы. Возникает вопрос, в каком случае путем замены переменных форму f привести к форме g? Это возможно, когда ранги матриц форм f и g равны и равны сигнатуры этих форм. Пусть f(х1, х2, …, хn)=(t²1+t²2+…+t²ℓ)= (t²ℓ+1+…+t²ℓ+k)

28.Прямая на плоскости. Виды уравнения прямой.

х= а1*t+x0

y=a2*t+y0-параметрическое задание прямой, t из R-параметр; М0(х0;у0); М(х;у); вектор а=(а1;а2)

Отсюда, t=x-x0/a1 и t=y-y0/a2

x-x0/a1=y-y0/a2-каноническое ур-е. Из этого можно олучить: 1/а1*х-1/а2*у+(у0/а2-х0/а1)=0, введем обозн.: А=1/а1, В=-1/а2, С= у0/а2-х0/а1.Тогда Ах+Ву+С=0-общее ур-е прямой. Из этого ур-я выразим у через х: Ву=-Ах-С, у= - А/В*х-С/В., введем обозн.: k= - А/В, b= - С/В. Тогда у=kx+b-ур-е прямой.

Из общего ур-я получаем: Ах+Ву= -С, Ах/-С+Ву/-С=1, х/--С/А+у/-С/В=1, введем обозн.: а= -С/А, b= -С/В. Тогда х/а+у/b=1- ур-е в отрезках.

29. Расстояние от точки до прямой на плоскости. Ах+Ву+Сz+D=0-ур-е плоскости. Расст. от точки до прямой обозн. ρ (ро)-перпендикуляр, опущенный из точки на плоскость.ρ = ׀Ах0+Ву0+Сz0+D׀/