- •1. Матрицы. Действия над матрицами
- •1Й индекс – номер строки
- •2Й индекс – номер столбца
- •1) Умножение матрицы на число
- •2) Сложение матриц
- •3) Вычитание матриц
- •4) Умножение матриц
- •5) Транспонирование
- •2. Свойства действий над матрицами
- •3. Определители 2-го и 3-го порядка
- •4. Свойства определителей
- •3) Если в определителе поменять местами 2 строки/столбца, то определитель изменит знак
- •4) Определитель с двумя пропорциональными строчками/столбцами равен нулю
- •5) Если вся строка/столбец определителя домножен на одно и то же число, то его можно вынести за знак определителя
- •6) Если в строку/столбец определителя добавить элементы параллельного ряда, домноженные на какое-либо число, то определитель не изменится.
- •5. Разложение определителя по строчке/столбцу. Минор. Алгебраическое дополнение
- •6. Обратная матрица
- •1) Считаем определитель detA≠0
- •2) Находим Aт
- •7. Ранг матрицы. Определение, свойства
- •8. Теорема Крамера
- •9. Метод Гаусса
- •10. Теорема Кронекера-Капелле
- •3) Если r матрицы системы меньше числа неизвестных, то система называется неоднородной и она имеет бесконечное множество решений.
- •11. Система однородных уравнений с n неизвестными
- •12. Векторы. Действия над векторами
- •1) Умножение вектора на число
- •2) Сложение
- •3) Разность
- •4) Скалярное произведение
- •13. Скалярное произведение: определение, выражение через координаты. Условия перпендикулярности векторов.
- •15. Векторное произведение: определение, выражение через координаты. Условия коллинеарности векторов.
- •Модуль этого вектора есть s параллелограмма, построенного на векторах a и b.
- •Вектор с перпендикулярен плоскости, в которой лежат a и b
- •Условия коллинеарности 2-х векторов.
- •16. Смешанное произведение векторов: определение, теорема, выражение через координаты. Условия компланарности векторов.
- •17. Линейная (не)зависимость векторов
- •18. Частные случаи линейной зависимости векторов
- •19. Базис
- •1) Они линейно независимы
- •2) Любой вектор можно представить в виде их линейной комбинации
- •20. Координаты вектора в ортонормированном базисе. Выражение |a| через координаты
- •1) Базисные векторы имеют единичную длину
1. Матрицы. Действия над матрицами
Матрица – таблица чисел, занумерованных следующим образом
a11 a12 … a1n
a21 a22 … a2n
…
am1 am2 … amn
1Й индекс – номер строки
2Й индекс – номер столбца
Аналогичная запись А=(Аmn)
Действия над матрицами
1) Умножение матрицы на число
Чтобы умножить матрицу на число, надо все ее элементы умножить на число
2) Сложение матриц
Складывать можно только матрицы одинаковой размерности. Складываем соответствующие элементы
3) Вычитание матриц
Аналогично сложению
4) Умножение матриц
Операция определена только для согласованных матриц (кол-во столбцов в 1й матрице=кол-во строк во 2й матрице)
Каждая строчка первой матрицы умножается на каждый столбец 2й матрицы и суммируется
Пример
1 2 1 1 1 5 3 7
3 4 * 2 1 3 = 11 7 15 А*В=В*А
1 0 1 1 1
5) Транспонирование
Меняем строчки и столбцы матрицы местами



2. Свойства действий над матрицами
А+В=В+А А+(В+С)=(А+В)+С
А+0(нулевая матрица)=А А-А=0
E(единичная матрица)*А=А α(любое число)*(А+В)=αА+αВ
(α+β)*А=αА+ βА α*( β*А)= (α*β)*А= β*(α*А)
А*(В*С)=(А*В)*С (не менять местами) А*(В+С)=А*В+А*С
(А+В)*С=А*С+В*С
α*(А*В)= (α*А)*В= А*(α*В) (α – число, его можно переставлять)
(А+В)т=Ат+Вт
(А*В)т=Вт*Ат
Если А*В=В*А, то матрицы А и В перестановочные
3. Определители 2-го и 3-го порядка
для каждой квадратной матрицы мы можем посчитать число – определитель матрицы - по следующему правилу:
А=(а11)
det(A)=|A|=a11
A= a11 a12
a21 a22
det(A)= a11 a12= a11*a22-a12*a21
a21 a22
a11 a12 a13
a21 a22 a23 = a11*a22*a33+a21*a32*a13+a12*a23*a31-a31*a22*a13-a21*a12*a33-a23*a31*a11
a31 a32 a33
4. Свойства определителей
1) определитель, содержащий нулевую строку/столбец =0
2) определитель, содержащий 2 одинаковых строки/столбца =0
3) Если в определителе поменять местами 2 строки/столбца, то определитель изменит знак
4) Определитель с двумя пропорциональными строчками/столбцами равен нулю
5) Если вся строка/столбец определителя домножен на одно и то же число, то его можно вынести за знак определителя
6) Если в строку/столбец определителя добавить элементы параллельного ряда, домноженные на какое-либо число, то определитель не изменится.
5. Разложение определителя по строчке/столбцу. Минор. Алгебраическое дополнение
a11 a12 … a1k … a1n
a21 a22 … a2k … a2n
……………………
ai1 ai2 … aik … ain
an1 an2 … ank … ann
Минором элемента aik (Mik)определителя n-го порядка называется определитель n-первого порядка, который получается из исходного определителя вычеркиванием строки с №i и столбца с №k.
Алгебраическим дополнением элемента aik определителя n-го порядка называется
Aik=(-1)(i+k)*Mik
Алгебраическое разложение
a11 a12 a13
a21 a22 a23 = a11* a22 a23 - a12* a21 a23 + a13 * a21 a22
a31 a32 a33 a32 a33 a31 a33 a31 a32
6. Обратная матрица
Квадратная матрица называется невырожденной, если ее определитель ≠0
Теорема: Всякая невырожденная квадратная матрица имеет обратную
А-1*А=А*А-1=Е (единичная матрица)
Нахождение А-1
1) Считаем определитель detA≠0
2) Находим Aт
3) А*= A11 A21 A31
A12 A22 A32
A13 A23 A33
4) A-1=
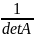 *
A*
*
A*5) А-1*А=А*А-1=Е
7. Ранг матрицы. Определение, свойства
Ранг матрицы А – наивысший порядок отличных от нуля миноров этой матрицы
r(A)=rang(A)
Свойства ранга:
1) r(A)≤min(m,n)
2) r(A)=0, если все элементы матрицы=0
3) A[nxn], r(A)=n, если det(A)≠0
8. Теорема Крамера
Рассмотрим систему из n уравнений и n неизвестных
a11*x1+a12*x2+…+a1n*xn=b1
a21*x1+a22*x2+…+a2n*xn=b2
…
an1*x1+an2*x2+…+ann*xn=bn
a11 a12 … a1n
∆= a21 a22 … a2n
…
an1 a2n … ann
a11 a12 … b1 … a1n
∆k= a21 a22 … b2 … a2n
…
an1 an2 … bn … ann
если
∆≠0, то система имеет единственное
решение: xk=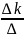 , где k=1,2,…,n
, где k=1,2,…,n
Если ∆=0 и хоть 1 из ∆k≠0, то решений нет.
Если ∆=0 и все ∆k=0, то Х-любое число.
a11 a12 … a1n x1 b1 A*X=B
A= a21 a22 … a2n X= x2 B= b2 ∆≠0
… … … A-1*AX=A-1*B
an1 an2 … ann xn bn EX=A-1*B
X=A-1*B
9. Метод Гаусса
Метод последовательного исключения неизвестных
Пример:
x1-x2+x3=3
2x1+x2+x3=11
x1+x2+2x3=8
1 -1 1 3 1 -1 1 3 1 -1 1 3 1 -1 1 3 1 -1 1 3
2 1 1 11 ~ 0 3 -1 5 ~ 0 1 -2 0 ~ 0 1 -2 0 ~ 0 1 -2 0
1 1 2 8 0 2 1 5 0 2 1 5 0 0 5 5 0 0 1 1
x3=1
x2-2x3=0 x1-2+1=3
x2=2 x1=4
x1=4
x2=2
x3=1
10. Теорема Кронекера-Капелле
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы = рангу расширенной матрицы системы
r(A)=r(A|B)
1) Если r(A)=числу переменных,. то система имеет 1 решение.
2) Если r(A)<n, то x1,x2,…,xr называются основными (базисными) переменными, если определитель из коэффициентов при них ≠ 0. Остальные n-r переменных называются свободными
3) Если r матрицы системы меньше числа неизвестных, то система называется неоднородной и она имеет бесконечное множество решений.
4) Решение системы, в котором n-r переменных =0, называется базисным.



11. Система однородных уравнений с n неизвестными
a11*x1+a12*x2+…+a1n*xn=0
a21*x1+a22*x2+…+a2n*xn=0
…
am1*x1+am2*x2+…+amn*xn=0
A*X=0
Всегда имеет минимум одно решение – нулевое.
m=n
Если m=n и при этом ∆≠0, согласно теореме Крамера, система имеет единственное нулевое решение.
Система линейных однородных уравнений имеет ненулевое решение, когда ранг ее матрицы меньше числа неизвестных.
r(A)<n
x1=k1, x2=k2, xn=kn – решение системы.
12. Векторы. Действия над векторами
Вектор – направленный отрезок. Нулевой вектор- начало и конец вектора совпадают (точка) Модуль вектора- длина отрезка АВ
Действия над векторами:
1) Умножение вектора на число
ʎ*a – число умножение на вектор а, есть вектор модуля, которого равен ǀʎ*aǀ = ǀʎǀ *ǀ аǀ, и направление совпадает с вектором а, если ʎ положит. И противополож. Направлению вектору а, если ʎ отрицательная.
2) Сложение
А)по правилу треугольника Б)по параллелограмму
3) Разность
a-b = a+(-1)b
4) Скалярное произведение
ab= ǀaǀ * ǀbǀ *cosµ
13. Скалярное произведение: определение, выражение через координаты. Условия перпендикулярности векторов.
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними.
(a,b)=|a|*|b|*cos(a,b) или (a,b)=xa*xb+ya*yb+za*zb
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
15. Векторное произведение: определение, выражение через координаты. Условия коллинеарности векторов.
axb=c
Векторное произведение двух векторов – вектор, которые обладает следующими свойствами:
Модуль этого вектора есть s параллелограмма, построенного на векторах a и b.
Вектор с перпендикулярен плоскости, в которой лежат a и b
с направлен таким образом, что если смотреть из его конца на плоскость a и b, то кратчайший поворот от 1-го вектора ко 2-му осуществляется против часовой стрелки (а, b, с взятые в указанном порядке образуют правую тройку)
Свойства векторного произведения:
1) axb=-bxa
2) (axb)xc≠ax(bxc)
3) ax(b+c)=axb+axc
Условия коллинеарности 2-х векторов.
a и b коллинеарны тогда и только тогда, когда axb=0
|axb|=|a|*|b|*sinµ
16. Смешанное произведение векторов: определение, теорема, выражение через координаты. Условия компланарности векторов.
a*b*c=(axb)*c
Смешанное произведение 3-х векторов по абсолютной величине равно V параллелепипеда, построенного на этих векторах
Условия компланарности 3-х векторов.
a b c компланарны тогда и только тогда, когда a*b*c=0
17. Линейная (не)зависимость векторов
Рассмотрим векторы a1,a2,…,an
Выражение вида α1a1+ α2a2+…+ αnan называется линейной комбинацией этих векторов
a1,a2,…,an называются линейно (не)зависимыми, если (не)существует равная нулю их линейная комбинация, в которой хотя бы 1 из коэффициентов α≠0
a1,a2,….,an линейно (не)зависимы, если (ни)1 из векторов (не)является линейной комбинацией остальных.
18. Частные случаи линейной зависимости векторов
1) n=2; Если a1 и а2 линейно зависимы, то они коллинеарны а1=α2а2
2) n=3; Если а1,а2 и а3 линейно зависимы, то они компланарны а1=α2а2+α3а3
19. Базис
а1,а2,…,аn образуют базис, если:
1) Они линейно независимы
2) Любой вектор можно представить в виде их линейной комбинации
3) линейная комбинация линейно независимых векторов=0
Теорема:
В трехмерном пространстве любые три линейно независимых вектора образуют базис.
20. Координаты вектора в ортонормированном базисе. Выражение |a| через координаты
Базис называется ортонормированным, если:
1) Базисные векторы имеют единичную длину
2) они взаимно ортогональны (т.е. перпендикулярны друг другу) |i|=|j|=|k|=1
a=ax*i+ay*j+az*k
Разложение а по базису векторов I,j,k
обозначим угол α, который образует вектор a с осью х, угол β – с осью у, угол µ - с осью z
ax=|a|*cos α; ay=|a|*cos β; az=|a|*cos µ
Координаты в ортонормированном базисе равны проекциям данного вектора на соответствующие оси координат, косинусы углов называются направляющими.
a{ax,ay,az}