6. Однородные системы линейных уравнений (ОСЛУ). Множество решений ОСЛУ как подпространство в Rn, его размерность. Базис подпространства решений (фундаментальная система решений) и запись общего решения ОСЛУ в форме линейной комбинации с неопределёнными коэффициентами.

СЛУ вида

называется однородным. М-мн-во решений ОСЛУ. Св-ва мн-ва М: 1. М - непустое мн-во. Одно из реш. ОСЛУ явл. реш. вида (0;0;…;0) значит, (0;0;…;0) ϵМ и поэтому М- непустое мн-во. 2. Сумма любых 2-х реш. ОСЛУ, как векторов, есть реш. этой системы. Значит, если (α1; α2;…;αn), (β1; β2;…;βn) ϵМ, то (α1+ β1; α2+; β2…;αn+ βn) ϵМ.

Покажем это. Пусть аs1х1+аs2х2+…+asnxn=0–S-е ур-е системы. Тогда as1α1+as2α2+…+asnαn=0 и as1β1+as2β2+…+asnβn=0-верные числ. равенства. Отсюда получаем, что as1(α1+β1)+ as2(α2+β2)+…+ asn(αn+βn)=0-верное числ. равенство, значит (α1+β1; α2+β2;…; αn+βn) ϵМ.

3. Произведение любого реш. ОСЛУ, как вектора на число(скаляр) есть реш. этой системы. Это означ., что если (α1; α2;…;αn) ϵМ и r ϵR, то (rα1; rα2;…;rαn) ϵМ.

Покажем это. Пусть аs1х1+аs2х2+…+asnxn=0–S-е ур-е системы. Тогда as1α1+as2α2+…+asnαn=0-верное числ. равенство. Отсюда as1(rα1)+ as2(rα2)+…+ asn(rαn)=0-верное числ. равенство. Значит, (rα1; rα2;…; rαn) ϵМ. При этом говорят, что мн-во М замкнуто относительно операций слож. векторов и умнож. вектора на скаляр. Заметим, что не все системы векторов обладают замкнутостью. Фундаментальной сист. реш. ОСЛУ(ФСРОСЛУ) назыв. базис(при усл. его существования) мн-ва реш. этой ОСЛУ.

7. Связь множества решений совместной неоднородной слу и соответствующей ей ослу, запись общего решения неоднородной слу.

Пусть даны 2 системы лин. ур-й:

a11x1+a12x2+…+a1nxn=b1

a21x1+a22x2+…+a2nxn=b2

…

am1x1+am2x2+…+amnxn=bm

и

a11x1+a12x2+…+a1nxn=0

a21x1+a22x2+…+a2nxn=0

…

am1x1+am2x2+…+amnxn=0-запись общего реш неоднородной СЛУ.

Пусть М-мн-во реш. ОСЛУ (γ1;γ2;…;γn)-частное реш. неоднородной СЛУ.

Пусть (α1;α2;…;αn) ϵМ. Покажем, что сумма векторов (α1;α2;…;αn)+ (γ1;γ2;…;γn) есть реш. неоднородной СЛУ.

Пусть as1x1+as2x2+…+asnxn=bs-S-е ур-е системы.

Тогда as1(α1+γ1)+ as2(α2+γ2)+…+ asn(αn+γn)= (as1α1+ as2α+…+ asnαn)+( as1γ1+ as2γ2+…+ asnγn)=0+bs=bs.

Отсюда получаем, что мн-во совместной неоднородной СЛУ получается как сумма всех реш. однородной сист. лин. ур-й с некоторым (частичным) реш. неоднородным СЛУ.

8. Скалярное произведение в Rn.

Рассм. отображение •: RⁿxRⁿ­­R (т.е отображение, обозначаемое •, паре векторов а и b из Rⁿ сопоставл. Число из R) со след. усл.: Для любых a, b, с ϵRn и любого числа αϵR справедливы равенства: 1. a*b=b*a 2. (α*a)b=α(a*b) 3. (a+b)c=a*c+b*c, при этом 4. a*a≥0 и a*a=0 при усл., что сам а= Ѳ Отображение назвы. скалярным произведением векторов из Rn. Из определения скалярного произведения следует, что справедливы равенства для любых векторов а, b ϵRn, и любых α и β ϵR. 1. a(α*b)=α*a*b и (α*a)*(β*b)=(α*β)*(a*b) 2. (a±b)* (a±b)=a*a+2ab+b*b 3. Ѳ*a=0

9. Неравенство Коши-Буняковского. Угол между векторами и длина вектора.

1) Пусть a, b ϵR и a≠ Ѳ, b≠ Ѳ. Для любого числа х ϵR справедливо: (a+x*b) (a*x+b)≥0. Тогда a²+2xab+x²b²≥0 или х²b²+2xab+а²≥0-квадратичное нерав-во, кот. справедливо для любого х ϵR. Отсюда получаем, что дискриминант этого нерав-ва ≤0. Значит (2ab)²-4a²b² ≤0 или 4(ab)²-4a²b², значит (ab)² ≤ a²b². Последнее неравенство назыв. нерав-во Каши-Бунековского. Заметим, что это неравенство справедливо в случае a= Ѳ или b= Ѳ. 2) Пусть а ϵRn, т.к а*а≥0, то существует арифметич. корень . Число назыв. длиной вектора а и обозн. ׀а׀. 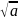׀а׀= ² Пусть а,b ϵRn и a≠ Ѳ, b≠ Ѳ, по нерав-ву К-Б получаем (ab)² ≤ a²b², отсюда (ab)²/ а²b²≤ 1 или -1≤ab/ ²* ²≤1. Получаем -1 ≤ab/׀a׀*׀b׀≤ 1. Величину arcсos ab/׀a׀*׀b׀ назыв. углом между векторами а и b и обозн. (a^b): 1. (a^b) ϵ[0, 180] 2. cos (a^b)=ab/׀a׀*׀b׀ 3. a*b=׀a׀*׀b׀* cos (a^b)

10. Ортонормированный и ортогональный базисы пространства. Выражение скалярного произведения векторов через их координаты в ортонормированном базисе. Пусть e1, e2,…,es–базис системы векторов М.Базис e1, e2,…,es –ортогональный; если скалярное произведение ei*ej=0, для всех i и j-1,…,s и i≠j. Говорят, векторы базиса ортонормированными, если: 1. ei*ej=0, для всех i и j-1,…,s и i≠j. 2. ׀ ei׀=1, для любого i-1,…,s (говорят, что векторы базиса-нормированы). Если a*b=0 для a, b ϵRn, то (a^b)=90 и при этом пишут, что вектор a перпендикулярен b. Как выглядит скалярное произведение векторов в ортогональном базисе: Пусть e1, e2,…,en-базис пространства Rn, кот. явл. ортонормированным. Пусть a, b ϵRn. Тогда a=α1e1+ α2e2+…+ αnen и b= β1e1+ β 2e2+…+ βnen. Вычисляем: a*b = (α1e1+ α2e2+…+ αnen)(β1e1+ β 2e2+…+ βnen)=…= (α1β1)e1e1+ (α2β2)e2e2+…+ +(αnβn)enen= α1β1 + α2β2 +…+ αnβn. ei*ej=0

16.Обратная матрица. Использование эквивалентных преобразований для нахождения обратной матрицы 1 0 … 0

0 1 … 0

0 0 … 1 _мхn

Матрица назыв. единичной и обозн. Е. Пусть А, В, Е ϵ Мn (R). Тогда справедливо А*Е=Е*А=А Матрица В назыв. обратной к матрице А, если А*В = В*А = Е. При этом пишут В=А^-1. Если для матрицы А сущ. обратная матрица, то матрицу А назыв. обратимой. Теорема: Пусть А ϵ Мn (R). Матрица А явл. обратимой тогда и только тогда, когда определитель матрицы А≠0. (׀А׀≠0) Способы вычисления обратной матрицы: 1) С помощью присоединения матрицы. Пусть А ϵ Мn (R) матрица вида:

А11 А12 … А1n

А21 А22 … А2n

...

Аn1 Аn2 … Аnn

где Aij- алгебр. доп-е к элем. матрицы А для всех i, j=1, …, n - назыв. присоединенной и обозн. А* Теорема: Пусть А ϵ Мn (R) и обратима. Тогда, А^-1= 1/׀А׀ х (А*)^Т 2) С помощью элементарных преобразований (метод черты). 1. перемена 2-х строк местами 2. умнож. строки на не нулевое число 3. прибавление одной строки к др., умножение на число. Пусть А ϵ Мn (R). Рассм. матрицу, кот. получается «склеиванием» матрицы А с Е, принадлежащей тому же мн-ву (Мn (R)), кот. обозн.: (А׀Е) Теорема: Если матрица А обратима, то с помощью элементарных преобр. матрицу (А׀Е) можно привести к матрице (Е׀А^-1). Т.к слева от черты нах-ся един. матрица, то справа от черты – обратная к А.