29.Парабола.
Парабла-ГМТ плоскости,равноудаленные от данной точки п-ти-фокуса и данной прямой называемой директрисой.
Y2=2pX –уравнение параболы
X2=2pY для вертикальной
Вершина параболы лежит на расстоянии P/2 между фокусом и директрисой параболы.
30.Кривые второго порядка.
1.Окружность
2.Эллипс
3.Парабола.
4.Гипербола.
31.Общее уравнение плоскости.Неполные уравнения плоскости.
Любая плоскость задается уравнением первой степени относительно x y z.
A(x-x0)+B(y-y0)+C(z-z0)+D=0
Ax+By+Cz+D=0 –общее уравнение плоскости.
Неполные уравнения- когда один или несколько коэффициентов в общем уравнении равны нулю.
D=0 –п-ть проходит через начало координат.
Если один из коэффициентов A B C равны нулю, плоскость параллельна оси, при которой коэффициент равен нулю.
Если два коэффициента равны нулю, включая D, то плоскость проходит через нулевую ось.
Если 2 координаты исключая D-плоскость параллельна плоскости нулевых координат.
Если 3 координаты включая D получаем уравнение ненулевой плоскости.
*Прим. Нулевая –та, в уравнении при координате которой стоит ноль.
32.Уравнение плоскости через три точки.Уравнение в отрезках.
Уравнение
в отрезках:
Выводится из общего уравнения путем подстановки нулей вместо координат.
Уравнение плоскости, проходящей через три известные точки.
Общее Уравнение получаем путем вычисления определителя данной матрицы.
33.Нормальное уравнение плоскости. Расстояние от точки до плоскости.
p-расстояние от начала координат до плоскости.
Косинусы-направляющие косинусы нормали.
D(M0
a)=
34.Уравнение прямой в пространстве.Переход от одного вида к другому.
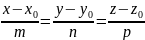–уравнение
прямой,проходящей через данную точку,
парлельно данному вектору.
Параметрическое уравнение:
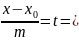x=mt+x0
y=nt+y0
z=pt+z0
Переход от общего уравнения к каноническому.
Есть два уравнения плоскостей, пересекающихся по прямой, координата z которой ранва нулю.
Направляющий вектор прямой равен векторному произведению нормальных векторов плоскостей.
35.Взаимное расположение плоскостей и прямых в пространстве.
Плоскость: Ax+By+Cz+D=0
Прямая:
Прямая может лежать в плоскости
Am+Bn+Cp =0
Ax0+By0+Cz0+D=0
Прямая может быть параллельна плоскости:
Am+Bn+Cp =0
Ax0+By0+Cz0+D
0
Может пересекать плоскость
Am+Bn+Cp 0
T=-
Тогда координаты точки пересечения равны:
M0(mt+x0;nt+y0;pt+z0)
39.Комплексные числа.
Комплексные числа- область чисел C,каждое из которых можно представить как z=x+yi ,где х,у-вещественные числа, а i-мнимая единица.
Z’=x-yi –сопряженное числа Z
Z*Z’=X2+Y2 –действительное число.
Φ-аргумент числа Z=arctg y/x , -П<arg Z<П
40.Действия над комплексными числами в алгебраической форме записи.
Z1±Z2=(x1±x2)+i(y1±y2)
Z1*Z2=(X1X2-Y1Y2)+i(X1Y2+X2Y1)
Z1/Z2=
Формы записи комплексного числа.
Z=x+yi –алгебраическая форма записи.
41.Тригонометрическая форма записи комплексного числа.Формула Муавра.
Z=|Z|(cosф+I sinф), где ф-arg Z
Формула Муавра.
Zn=|Z|n(cos nф+i sin nф)
42.Показательная форма.Формула Эйлера.
Показательная форма числа.:
Z=|Z|eiф
Формула Эйлера:
е±iф= cosф±i sin ф
43. Ограничение множества. Теорема о достижении точкой верхней(нижней грани).
Множество ограничено,если существуют М≥0 такое,что нижняя граница равна –М, а врехняя +М.
Функция,непрерывная на отрезке, она достигает своей верхней и нижней точки.
44.Последовтельность.Предел последовательности.
Числовая последовательность-функция от натурального аргумента.
а- предел числовой последовательности xn, при котором n стремится к бесконечности, если для любого бесконечно млаой величины (e) есть такая N=N(e),при которой любое n>N => xn-a <e:
Lim xn=a
n->
Предел-окрестность определенной точки.
45.бесконечно малые и большие последовательности и их свойства.
Бесконечно малая последовательность-та,что стремится к нулю.
Бесконечно большая-та,что стремится к ±
Свойства:
1) Бесконечно малая последовательность является ограниченной последовательностью.
2) Любая конечная сумма бесконечно малых последовательностей есть также бесконечно малая последовательность.
3) Произведение бесконечно малой последовательности на любую ограниченную последовательность или на любое конечное, отличное от нуля, число есть бесконечно малая последовательность.
4) Линейная комбинация счетного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
5)Отношение бескоенчо малой к функции, имеющей конечный предел не равно нулю.