32. Определение графа, орграфа, мультиграфа и псевдографа

Определение. Графом G(V,E) называется совокупность двух множеств – непустого множества V и множества E неупорядоченных пар различных элементов множества V. Множество V называется множеством вершин, множество E называется множеством рёбер.

G(V,E) = <V,E>, V , E VxV.

Число вершин графа обозначим через p, число рёбер через q.

Пример. V = { }, E = { = ( ), = ( ), = ( ), = ( ), = ( )}, p = 4, q = 5.

Обычно граф называют диаграммой: вершины – точками, рёбра – линиями.

Пример.

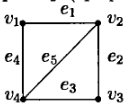
Определение. Если элементами множества E являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E – дугами. На диаграмме дуги изображаются стрелками.

Пример. V = { }, E = { = { }, = { }, = { }, = { }, = { }},

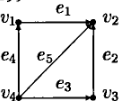
Определение. Если элементами множества E могут быть пары одинаковых элементов V (v,v), то такой элемент называется петлей, а граф псевдографом.

Определение. Если E не множество, а семейство, то есть если E содержит одинаковые элементы, то такие элементы называются кратными рёбрами, а граф называется мультиграфом.

33. Степень вершины. Лемма Эйлера. Теорема о числе вершин нечетной степени

Определение. Пусть - вершины, e = ( ) – соединяющие их ребро. Тогда вершина и ребро e инцидентны, вершина и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается Г(v): Г(v) = {u V: (u,v) E}. Если A V – множество вершин, то Г(A) – множество всех вершин, смежных с вершинами из A: Г(A) = Г(v).

Пример. В этом графе вершины и , и , и , и , и смежные, а вершины и не смежные. Рёбра и , и , и , и , и , и , и , и смежные, и , и не смежные.

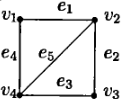
Определение. Количество рёбер, инцидентных вершине v, называется степенью (или валентностью) вершины v и обозначается d(v).

Определение. Если степень вершины равна 0, то вершина называется изолированной. Если степень вершины равна 1, то вершина называется висячей.

Определение. Для орграфа число дуг, исходящих из вершины v, называется полустепенью исхода , а входящих – полустепенью захода .

Лемма (Эйлера). Сумма степеней вершин графа равна удвоенному количеству рёбер

, .

Доказательство. При подсчёте суммы степеней вершин каждое ребро учитывается два раза.

Теорема о числе вершин нечётной степени. Число вершин нечётной степени в графе чётно.

Доказательство. В противном случае сумма степеней вершин была бы нечётной, что противоречит лемме Эйлера.

34. Смежность вершин и ребер графа. Матрица смежности.

Определение. Пусть - вершины, e = ( ) – соединяющие их ребро. Тогда вершина и ребро e инцидентны, вершина и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается Г(v): Г(v) = {u V: (u,v) E}. Если A V – множество вершин, то Г(A) – множество всех вершин, смежных с вершинами из A: Г(A) = Г(v).

Пример. В этом графе вершины и , и , и , и , и смежные, а вершины и не смежные. Рёбра и , и , и , и , и , и , и , и смежные, и , и не смежные.

Определение. Количество рёбер, инцидентных вершине v, называется степенью (или валентностью) вершины v и обозначается d(v).

Определение. Если степень вершины равна 0, то вершина называется изолированной. Если степень вершины равна 1, то вершина называется висячей.

Определение. Для орграфа число дуг, исходящих из вершины v, называется полустепенью исхода , а входящих – полустепенью захода .

Рассмотрим граф G(V,E) с p вершинами и q рёбрами.

1. Матрица смежности. Так называется матрица M: p x p,

Это определение подходит и для орграфа D(V,E).

Пример.

G : D:

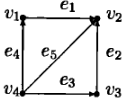
Приведём основные свойства матрицы смежности

1) Матрица смежности неориентированного графа симметрична .

2) Сумма элементов матрицы M(G) по i-ой строке (по i- му столбцу) равна степени i-й вершины:

3) Суммы элементов матрицы M(D) по i-й строке и по i-му столбцу соответственно равны полустепени исхода и полустепени захода i-ой вершины

.

35. Инцидентность вершин и ребер графа. Матрица инцидентности

Определение. Пусть - вершины, e = ( ) – соединяющие их ребро. Тогда вершина и ребро e инцидентны, вершина и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается Г(v): Г(v) = {u V: (u,v) E}. Если A V – множество вершин, то Г(A) – множество всех вершин, смежных с вершинами из A: Г(A) = Г(v).

Пример. В этом графе вершины и , и , и , и , и смежные, а вершины и не смежные. Рёбра и , и , и , и , и , и , и , и смежные, и , и не смежные.

Определение. Количество рёбер, инцидентных вершине v, называется степенью (или валентностью) вершины v и обозначается d(v).

Определение. Если степень вершины равна 0, то вершина называется изолированной. Если степень вершины равна 1, то вершина называется висячей.

Определение. Для орграфа число дуг, исходящих из вершины v, называется полустепенью исхода , а входящих – полустепенью захода .

Матрица инциденций. Так называется матрица H: p x q,

для неориентированного графа:

для ориентированного графа:

Пример.

Приведём основные свойства матрицы инцидентности

1. Сумма строк матрицы H(D) является нулевой строкой.

2. Сумма строк матрицы по модулю 2 H(G) является нулевой строкой

36. Типы графов: пустой, полный, регулярный, двудольный

Определение. Граф G(V,E) называется пустым, если E = .

Определение. Граф G(V,E) называется полным, если в нём любые две вершины смежные, то есть . Полный граф определяется числом своих вершин и обозначается , где n = |V|. Полный граф имеет максимально возможное число рёбер: q( )=p(p-1)/2.

Определение. Если степени всех вершин равны k, то граф называется регулярным степени k.

Определение. Граф G(V,E) называется двудольным, если множество V можно разбить на два непересекающихся подмножества и : , таким образом, что любое ребро из E соединяет вершину из с вершиной из . Множества и называются долями двудольного графа. Если двудольный граф содержит все возможные рёбра, то есть , то он называется полным двудольным графом и обозначается , где m=| |, n=| |.