Варианты извлечения сверхприбыли при идеальной дискриминации

Полное изъятие ренты:

а) цена соответствует максимальной оценке покупателя, P=v, если v - ценность товара

б) У покупателей одинаковые функции спроса с отрицательным наклоном

n - кол-во покупателей

Спрос каждого: q=D(p)/n

Совокупный спрос (известен монополисту) q=D(p)

Полнота изъятия ренты зависит от ценовой шкалы.

Ценовая шкала - это общая сумма денег (T), зависящая от объема покупки(q)

Ценовая шкала соответствует единой цене T(q)=pq

Линейная ценовая шкала

П=p^m*q-Cq=p^m*D(p^m)-C (D(p^m))

Нелинейная ценовая шкала

еще премия, которую платит покупатель за право купить товар по более низкой цене. Она может достигать размера выигрыша потребителя

T(q)=A+pq

A - премия

Если монополист использует шкалу конкурентных цен, тогда чистый излишек покупателей - сумма всех излишек

используя нелинейную ценовую шкалу или двухставочный тариф

T(q)=pq+A (S^c/n)

Монополист получает прибыль:

П= S^c+p^c*q^c-C(q^c)

Вывод: Прибыль от конкурентных цен и премии больше, чем прибыль от монопольных цен p^m*q^m-C(q^m), так продукции продается больше.

3) правила обратной эластичности

* арбитраж между покупателями невозможен

*функции спроса с отрицательным наклоном

*рынок поделен на m сегментов

Прибыль монополиста максимизируется путем подбора цен по правилу обратной эластичности

прибыль монополиста обратно пропорциональна коэффициенту эластичности

объем выручки-объем издержек

Оптимальная цена требует, чтобы монополист взимал большую плату за товар на том рынке, где спрос менее эластичен

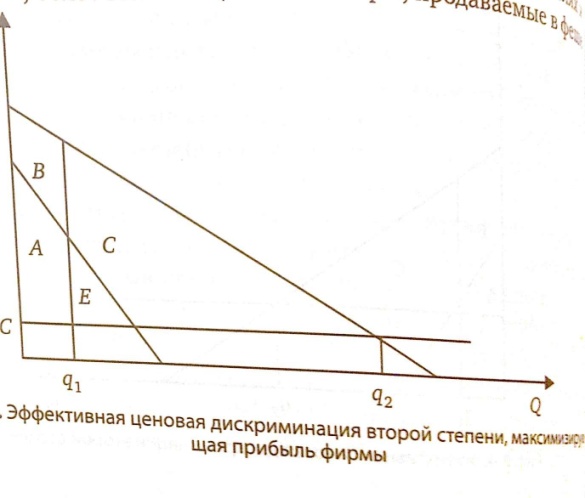
16. Функции спроса и извлечение сверхприбыли при ценовой дискриминации второй степени.

Для того, чтобы осуществить ценовую дискриминацию второй степени, монополист должен суметь разделить спрос, предъявляемый на рынке неоднородными потребителями, на   частей   Предположим, что прямые сигналы о предпочтениях потребителей отсутствуют, поэтому рассортировать покупателей по группам он сразу не сможет. Однако, неоднородные потребители обладают все же некоторыми скрытыми характеристиками, которые и может использовать производитель. Он может предложить всем покупателям ценовой прейскурант, в котором цена зависит от какого-либо параметра (количество, качество, время и т. д.), предоставляя им возможность выбора наиболее приемлемого для них набора (цена – количество, цена – качество и т. д.). Таким образом, он принуждает потребителей к самоотбору. В итоге фирма окончательно может предложить два набора: набор q1 по цене А и набор q2 по цене А+С+Е (рис.9.5.). Эти наборы с одной стороны эффективны с точки зрения самоотбора покупателей, а с другой стороны, они максимизируют прибыль фирмы.

Часто ценовая дискриминация второй степени проводится в виде сочетания не количества, а качества товара с определенной ценой ( высокие цены на самолеты 1-го класса, обслуживание в 5-х отелях и ресторанах).

Цель подобного рода дискриминации – стимулировать самоотбор покупателей, т.е. вынудить тех, кто может платить за высокое качество обслуживания, действительно отдать эти деньги.

21. Многорыночная ценовая дискриминация (третьей степени).

Многорыночная ценовая дискриминация основана на прямых сигналах о предпочтениях покупателя (пол, возраст, положение в обществе, местонахождение, который раз покупает товар, уровень дохода и т.д.) – рынок делится на сегменты.

Связана с правилом обратной эластичности (inverse-elasticity rule):

Условия модели:

1. Рынок разделен на m сегментов на основе информации о потребителе

2. Функции спроса отрицательным наклоном

3. Не возможен арбитраж покупателей внутри и между сегментами

Объемы спроса на каждом сегменте:

q₁ = D₁(p₁), … q_i = (D_i(p_i), … q_m= D_m(p_m).

Совместный спрос: q = Σ D_i(p_i)

Прибыль монополиста: Σ p_i D_i(p_i) – С [Σ D_i(p_i)], (т.е. pq – Cq ) максимизируется путем подбора цен по правилу обратной эластичности:

для каждого сегмента рынка i выполняется равенство:

Pi – C(q)/ Pi = 1/ E_i , где E_i = D_i(p_i) p_i / D_i(p_i) – коэф-т эластичности спроса на i-ом сегменте рынка.

Правило обратной эластичности:

Оптимальная цена требует, чтобы монополист взимал большую плату за товар на том рынке, где спрос менее эластичен.

22. Правило обратной эластичности.

Оптимальная цена требует, чтобы монополист взимал большую плату за товар на том рынке, где спрос менее эластичен. То есть возникает в связи с максимизацией прибыли.

(Pi-C’)/Pi = 1/Ei; Ei = - Di’(Pi)*(Pi/D(Pi)) = - (qi*pi)/qi

(i подстрочное)

23. Ценовая дискриминация и общественное благосостояние. Проблема «справедливой цены».

Приносит ли выигрыш обществу ценовая дискриминация третьей степени?

Предположим, что монополист не дискриминирует цена усредняется.

Тогда сегмент рынка с низкой эластичностью (Е < 0 ) выигрывает, т.к. Р понижается. На высокоэластичном сегменте рынка Р повышается.

Более бедные покупатели уходят с рынка и он резко сужается или исчезает.

Эффект от «справедливой цены»:

- устанавливается за счет покупателей на дешевом рынке (более бедных);

- дешевый сегмент рынка может свернуться;

- выигрыш производителя на обоих рынках сокращается.

Как изменится общественное благосостояние после усреднения цены?

Допущения модели:

1)постоянные издержки от масштаба

2)Цена монополиста при дискриминации – p_i (на рынке i), спрос - q_i = D_i(p_i);

3)Общий чистый выигрыш покупателей: Σ Si (pi);

4)прибыль монополиста: Σi (pi – c)qi, где c – предельные издержки

При отмене дискриминации:

1)Усредненная цена - р_ср,

2)функция спроса - q_{i ср.} = D_i(p _ср.) на i-том рынке;

3)Прибыль мон-та (без дискр): Σ (p_ср – c)q_{i ср}

 

4)Общий выигрыш покупателей (на всех сегментах) при р _ср составит: Σ Si (p_cp);

5)∆q Ξ q_i – qi_cp .

Разница в благосостоянии общества при введении дискриминации (∆W) составит:

изменение в выигрыше покупателя плюс изменение в прибылях производителя:

∆W = ( Σ[Si (pi) - Si (p_cp)] )+( Σ (pi – c)qi - Σ (p_ср – c)q_{i ср} )

Верхняя и нижняя границы изменения общественного благосостояния:

А) Нижняя граница: : ∆W ≥ Σi (p_i – c) ∆qi

при условии, что Si (pi) - Si (p_cp) ≥ S_i´(p_ср) х (p_i – pcp),

Из неравенства (А) следует, что ценовая дискриминация :

увеличивает общественное благосостояние.

ведет к улучшению эффективности распределения по Парето.

увеличивает прибыль монополиста, появляется выигрыш покупателя на втором (дешевом) рынке, а выигрыш покупателя на первом рынке не изменяется.

Б) Верхняя граница: ∆W ≤ (p_cp – c)( Σi∆qi )

при условии, что Si (p_cp) - Si (pi) ≥ S_i´(p_i) х (pcp – p _i)

Из неравенства (Б) следует, что ценовая дискриминация уменьшает обществ. благосостояние, если она не увеличивает общий выпуск (total output) продукции.

Такая ценовая дискриминация вызывает различия в предельных нормах замещения среди покупателей и поэтому менее предпочтительна, чем единая (усредненная) цена

(если цель общества – перераспределение данного кол-ва продукции).

Заключение:

влияние ценовой дискриминации третьей степени на общественное благосостояние неоднозначно:

- С одной стороны, с появлением более дешевого рынка монополист повышает прибыль, а покупатели – свой выигрыш за счет дорого сегмента рынка.

- С другой стороны, покупатели на дорогом сегменте рынка, как правило, заметно богаче и такая дискриминация вряд ли уменьшает эффективность перераспределения доходов.

Заявление, что ценовая дискриминация снижает обществ.благосостояние основывается на сохранении всех рынков после отмены дискриминации.

Однако если при усреднении цены дешевый рынок уничтожится (покупатели не захотят платить по повышенной цене), то на рынке с низкой эластичностью установится чистая монополия и ср.цена станет монополистической, выпуск сократится.

24. Ценовая дискриминация третьей степени, основанная на различиях в местонахождении покупателей (пространственная дискриминация).

Удаленность от продавца:

Условия модели:

Производитель сам перевозит товар и транспортные изд.включает в цену р(х)

Транспортные издержки на единицу товара - (t) составляют tx для покупателя на расстоянии x, тогда цена при самовывозе - р(х) – tx.

Несколько покупателей на разном расстоянии, но с одинаковой ф-ей спроса q = D(p).

Для равноудаленных покупателей цена одинакова и прибыль производителя максимальна, если максимизируется (р – tx – с) D(p).

Транспортные издержки эквивалентны акцизам:

цена покупателя – р,

а цена продавца – р – tx.

1. линейная функция спроса - производитель берет на себя половину суммы, на которую вырос налог.

2. При экспоненциальной функции спроса покупатель полностью берет на себя возросшую сумму налога.

3. Если эластичность спроса const, покупатель оплачивает даже больше, чем сумма, на которую возрос налог

Пусть расстояние до покупателя увеличивается. Тогда монопольная цена возрастет, но в зависимости от вида функции спроса :

а) ∆p = t ∆x - при экспоненциальной функции;

б) ∆p = t ∆x/2 при линейной функции спроса;

в) ∆p = t ∆x/ (1 - 1/Е) - в случае спроса с эластичностью const.

- Экспоненциальная функция спроса - не дает провести ценовую дискриминацию, т.к. любое изменение в издержках сразу повлияет на цену поставки (монополист использует цену f.o.b., одинаковую для всех покупателей).

- Линейная функция спроса - покупатель оплачивает не все транспортн. издержки, а монополист проводит политику «freight absorption» (берет на себя расходы по доставке).

Продавая всем по одной цене, монополист дискриминирует против близких покупателей

• При спросе с постоянной эластичностью -дискриминация против наиболее удаленных покупателей (т.к. растут транспортные издержки монополиста, а покупатель никуда не денется).

А что на практике?

Возможность арбитражирования между покупателями, практически исключает использование ценовой дискриминации при спросе с постоянной эластичностью. Если транспортные средства доступны, то покупатели будут перепродавать товар в более удаленные районы. Поэтому в основном практикуется дискриминация, связанная с политикой «freight absorption».

Почему широко используется «freight absorbtion»?

эластичность спроса у более дальнего покупателя увеличивается из-за доступности альтернативных поставщиков.

( Например, два цементных завода –

в 100 км друг от друга.

Эластичность спроса у покупателя, находящегося в 50 км, больше, чем у покупателя, находящегося в 10 км от 1-го завода и 90 км от 2-го завода.)

Приложение к линейной функции спроса.

Предположим, что функция спроса на i-ом рынке qi = ai – bip, ai > c bi (это условие обеспечивает функционирование всех рынков при введении дискриминации).

Монополист выбирает такую цену pi, чтобы максимизировать прибыль

(pi – c) qi или (pi – c)( ai – bip).

Тогда оптимальная цена:

pi = (ai + cbi)/2bi

Оптимальный выпуск: qi= (ai – cbi)/2.