14) Логарифмические уравнения . Способы их решения :

- такие уравнения, в которых неизвестная величина находится под знаком логарифма

А) =

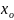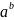
Б) x = L , где L = => x = L

15) Показательное неравенство. Методы их решения :

- называются неравенства содержащие переменные с показателем степени

Простейшими показательными неравенствами явл неравенства вида :

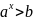
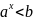( a ≠ 1 , a > 0 )

Методы решения:

1. >

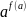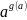
1. Если a > 1 , то исходное неравенство равносильно неравенству f(a) > g(a)

2. 0< a < 1 a в пределах от 0 до 1 сходное неравенство равносильно неравенству f(a) < g(a)

2. >

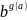
16) Логарифмические неравенства. Методы их решения

- простейшими логарифмическими неравенствами называются неравенства вида:

x > b x < b

Методы решения:

1. Неравенства вида f(a) > g(a)

А) при a > 1 это неравенство равносильно системе неравенств f(a) > 0 , g(a) > 0 ; F(а) > g(a)

Б) при 0 < a < 1 неравенство равносильно системе неравенств f(a) > 0 , g(a) ; f(a) < g(a)

2) Применение свойств логарифма

3) Замена переменной

17) Рациональные неравенства. Методы их решения :

- у которого левая и правая часть являются рациональным выражением

Методы решения :

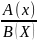1. > 0

Левую и правую часть необходимо умножить на 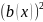.В результате получим исходное неравенство

A(x) * B(x) > 0

Можно решить методом интервалов

2. >

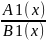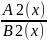
Необходимо все перенесите в левую часть

18) Иррациональные неравенства. Методы их решения:

Если в неравенство под знаком корня входит неизвестное, то такое неравенство иррациональное

Метод решения:

Заключается в возведении обеих частей неравенства в нужную степень. Возводить в квадрат не нарушая равносильности можно только неравенству , у которого обе части неотрицательны

При возведении квадрат неравенств, левые и правые части которого имеют нерав знаки , могут получится неравенства как равносильны исходному так и не равносильны исходному

19) Методы интервалов . Решение неравенств :

Метод интервалов:

1. На оси 0(x) отметить точки x1,x2….xn

2. Над интервалами справа налево расставить по очереди знаки + -, начиная со знака +

3. Множеством решением неравенства (x-x1) (x-x2)….(x-xn) > 0является объединение интервалов со знаком+

4. Множеством решением неравенств (x-x1)(x-x2)…..(x-xn) <0 является объединение интервалов со знаком –

20) Система уравнений. Методы их решений:

- решением системы называется пара чисел (Xo, Yo) при подстановки которых соот. Место х и у каждое уравнение системы образуется в верное равенство

Методы решения:

1. Метод подстановки позволяет свести систему уравнений с 2 неизвестными к 1 уравнению с 1 неизвестной

Из одного уравнение выраж. неизвестной х или у и подставляется в другое уравнение

2. Метод исключения неизвестного. Заключается в том, что с помощью последовательного исключения неизвестного система уравнений сводится к уравнению с одним неизвестным.

3. Метод замены неизвестного

4. Способ сложения и вычитания. Сначала необходимо уровнять в обоих уравнениях коэффициент при каком-нибудь неизвестном. Затем оба уравнения необходимо сложить, если коэффициенты разные знаки и вычесть, если имеют одинаковые знаки

5. Способ умножения

6. Графический способ. Из каждого уравнения необходимо выразить у как функцию от х

Y = f(x) Начертить графики 2 функций

1. Если графики имеют точки пересечения, то абсцисса х , то ордината у

2. Если линия окажется параллельной , то решения нет

3. Если линии сливаются в одну, то система считается неопредел. и имеет множество решений

4. Система симметричных уравнений .Используется замена