Корень степени n:
Корнем степени n из числа b называют такое число а, n степень которого равно b
Нахождение корня n степени из числа b называют извлечением корня. Результат извлечения корня называют радикалом.
Корни четной и нечетной степени:
N=2m+1 – нечетная степень. m€n
а) корень нечетной степени из положительного числа является положительным числом :
если
b
>0 , то
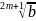> 0
б) корень нечетной степени из отрицательного числа будет отрицательным:
если b< 0 , то <0
в) корень из нечетной степени из 0 , равен 0 :
если в= 0, то = 0
n = 2m , m € n – четная степень
а) корень четной степени из положительного числа имеет 2 значения противоположенные по знаку :
если
b
> 0 , то
:
±
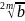б) корень четной степени из нечетного числа не существует:
если b < 0 , то – не существует
в) корень четной степени из 0 равен 0
если в=0 , = 0
Арифметический корень и его свойства:
Арифметический корень – неотрицательный корень степени n из неотрицательного числа называется арифметическим корнем
а)
если b
≥ 0 , то
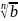будет являться арифметическим корнем
б) если b < 0 и корень нечетной степени , то этот корень называется корень степени n , но он не является арифметическим корнем
в) b < 0 , то – не существует
4) Свойство корней степени n :
1)
=
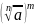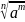
2)
=
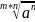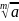
3)
=
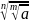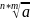
4)
=
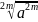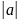
5) Степень с рациональным показателем :
а
=
=
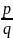, a>
0
– рациональный показатель
q€ n , q > 1
Число
в степени
–арифметический корень степени q
из числа
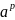
p- целое число
формулы
: a
=
=
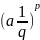
a
=
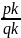a
=
=
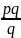6) Свойство степени с рациональным показателем :
1)
a
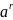> 0 :
> 0
Число а в степени с любым рациональным показателем –положительно
2) а > 0 , r1 и r2 – рациональны
а)
При умножении степени с рациональным
показателем одного и того же числа а
показатели степеней складываются
*
=
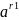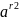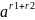
б)
При делении степеней с рациональным
показателем одного и того же числа а
показатели степеней вычитаются
=
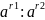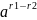
в)
При возведении степени с рациональным
показателем числа а в другую рациональную
степень показатели степеней перемножаются
=
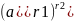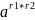
3)
а) степень с рациональным показателем
произведения 2 чисел равно произведению
тех же степеней со множителем
=
*
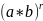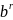
б)
Степень с рациональным показателем
частного двух чисел равна частному тех
же степеней делимого и делителя
=
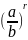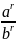
4) a > 1 , r- рациональное
а) > 1 , при r > 0
б) 0< < 1 , при r < 0
5)
a > 1
<
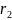
6) 0< a < 1 <
7)
Функция у=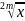
,
. Свойство:
Функция
у =
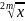Свойство :
1) Если x > 0 , то y > 0
2) Если х = 0, то у = 0
3) Функция возрастает
4) Функция непрерывна
5) Если х стремится к бесконечности, то у тоже
Функция
у =
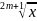Свойство :
1)Область определения функции: ( -∞;+∞)
2) Общее значение функции : (-∞;+∞)
3) Функция возрастающая
4) Функция непрерывна
5) Функция нечетная