Сила зв’язку

Коефіцієнт кореляції	Сила зв'язку
От±0, 81 до±1,00	Сильна
Від ±0,61 до ±0, 80	Помірна
От±0,41 до±0,6	Слабка
Від ±0,21 до ±0,4	Дуже слабка
От±0,00до±0,19	Відсутня

Знайдемо щільність зв'язку між залежною величиною Y і незалежною X. Тобто запитаємо себе, наскільки значним є вплив змінної X на Y? Критерієм, що допомагає отримати кількісну оцінку цього впливу є коефіцієнт кореляції:

(3.19)

Вираз для дисперсій має наступний вид:

(3.20)

Частина дисперсії, що пояснює регресію, називається коефіцієнтом детермінації і позначається - R. Коефіцієнт детермінації використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної X.

Таким чином, коефіцієнт детермінації можна за­писати у вигляді двох виразів, які є еквівалентними:

(3.21)

Коефіцієнт детермінації завжди додатний і знаходиться в межах від нуля до оди­ниці (0≤R²≤1).

Кожна сума квадратів пов'язана з числом, яке називають її "ступенем вільності". Це число показує, скільки незалежних елементів інформації, що утворились з елементів у₁ і, у₂,..., y_n, потрібно для роз­рахунку даної суми квадратів.

У статистиці кількістю ступеня вільності пев­ної величини часто називають різницю між кількістю різних дослідів і кількістю констант, знайдених завдяки цим дослідам незалежно один від одного. Окреме застосування цього поняття відноситься до суми квадратів.

Ступені вільності прийнято позначати через DF, або dF, або df.

У разі простої лінійної регресії ступені вільності, як і суми квадратів, можна розкласти таким чином:

n – 1 = 1 + (n – 2) (3.22)

Перевірка моделі на адекватність за F-критерієм Фішера складається з певних етапів:

1) На першому етапі розраховуємо величину, так зване F-відношення:

(3.23)

де MSR - середній квадрат, який можна пояснити з регресійної моделі;

MSE - середній квадрат помилок; 1, (n - 2) - ступені вільності, відповідно пов'язані з MSR і MSE.

2) На другому етапі задаємо рівень значимості або α100%. Наприклад, якщо ми вважаємо, що мож­лива помилка α для нас становить 0.05 (або 5%), це означає, що ми можемо помилитися не більш, ніж у 5% випадків, а в 95% випадків (або в 100*(1 - α)% ) наші висновки будуть правильними.

3) На третьому етапі за статистичними таблиця­ми F-розподілу. Фішера з (1, n - 2) ступенями вільнос­ті та рівнем значимості 100*(1 - α)% знаходимо критичне значення (F_кр).

4) Якщо розраховане нами значення F > F_кр, то ми відкидаємо гіпотезу Н_о, що β₁ = 0 (або що (ŷ_і = ), з ризиком помилитися не більше ніж у 5% випадків.

Отже, якщо F > F_кр, то побудована нами регресійна модель адекватна реальній дійсності.

Розглянемо порядок розробки та застосування моделі на прикладі розв'язання конкретного завдання аналітичного дослідження щодо визначення впливу фактору часу на показники обсягу реалізації товарної продукції підприємства ПП «Багіра СВ».

Вихідними даними для розрахунку будуть квартальні показники обсягу реалізації товарної за період з 2006 по 2008 роки.

Введемо початкові дані в таблицю Excel. За допомогою статистичних функцій Отрезок та НАКЛОН і зробимо оцінку методу найменших квадратів та побудуємо рівняння лінійної регресії для обсягу реалізації товарної продукції (див. рис. 3.2).

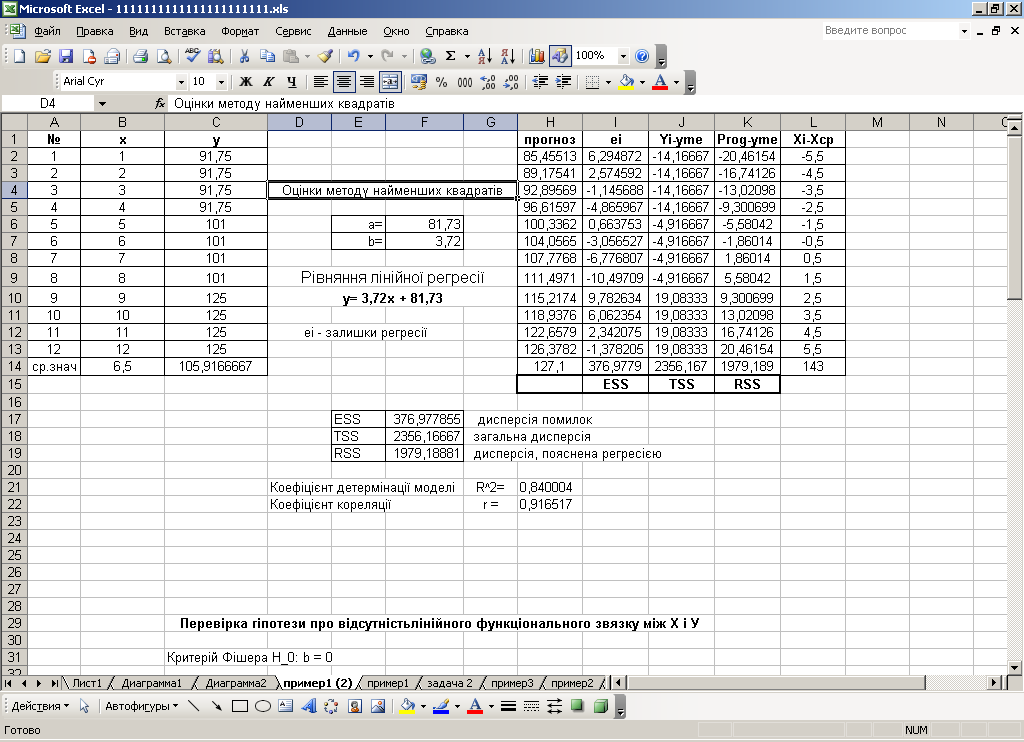
Рис. 3.2. Розрахунок параметрів лінійної моделі для обсягу реалізації товарної продукції

Далі проводимо розрахунки: е_і – залишків регресії, ESS - дисперсії помилок, TSS - загальної дисперсії та RSS - дисперсії, що пояснена регресією. Дані розрахунків представлені на рис. 3.3.

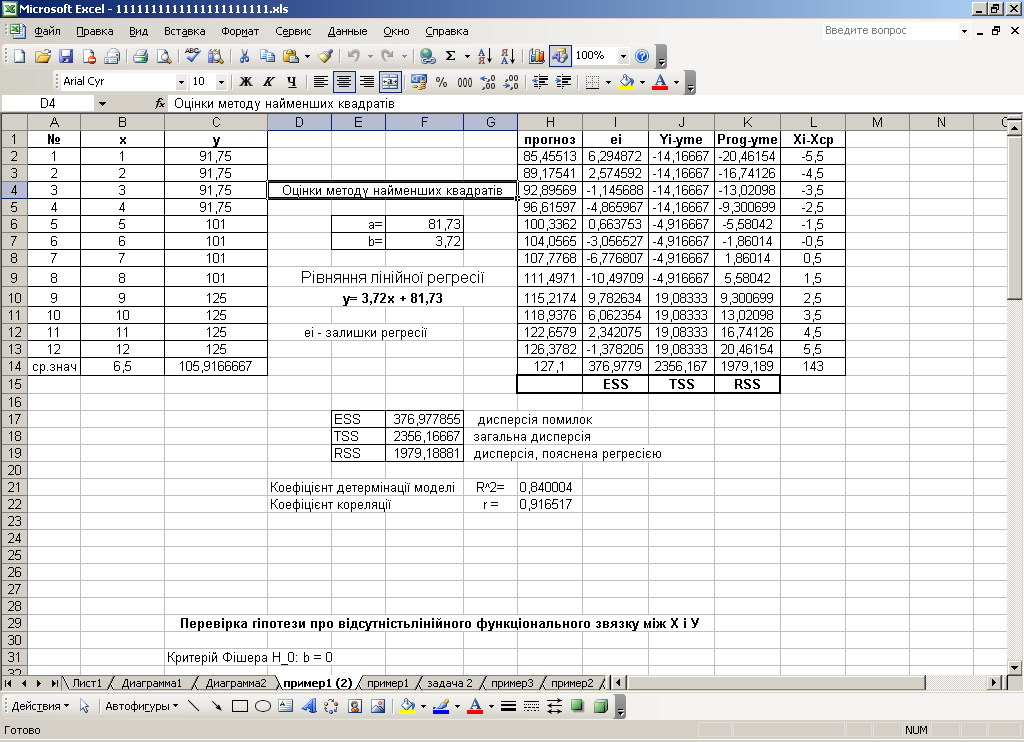
Рис. 3.3. Дані розрахунків залишків регресії, дисперсії помилок, загальної дисперсії та дисперсії, що пояснена регресією для обсягу реалізації товарної продукції

Далі розрахуємо коефіцієнт детермінації моделі R², він дорівнює: 0,840.

Розрахуємо коефіцієнт кореляції r = КОРЕНЬ (R²) =0,916.

Проведемо перевірку гіпотези про відсутність лінійного функціонального зв’язку між Х і У. Дані розрахунків наведено на рис. 3.4.

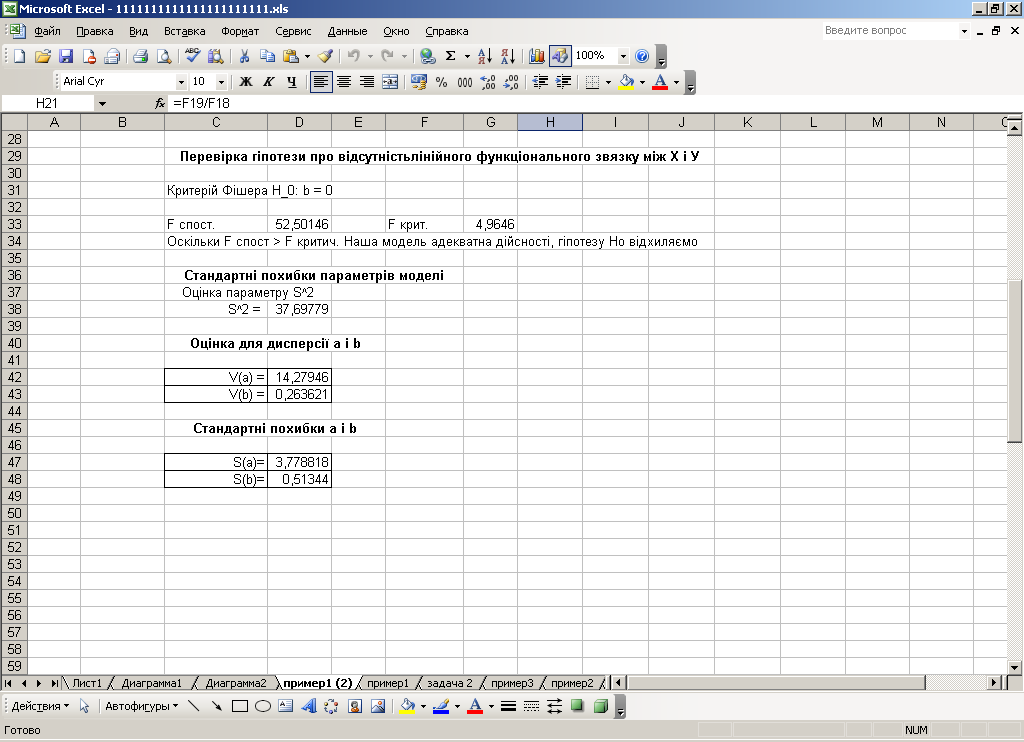
Рис. 3.4. Перевірка гіпотези про відсутність лінійного функціонального зв’язку між Х і У для показників обсягу реалізації товарної продукції

Достовірність усіх розрахунків перевіримо за допомогою інструмента Регрессия у табличному процесорі Excel. Результати представлені на рис. 3.5.

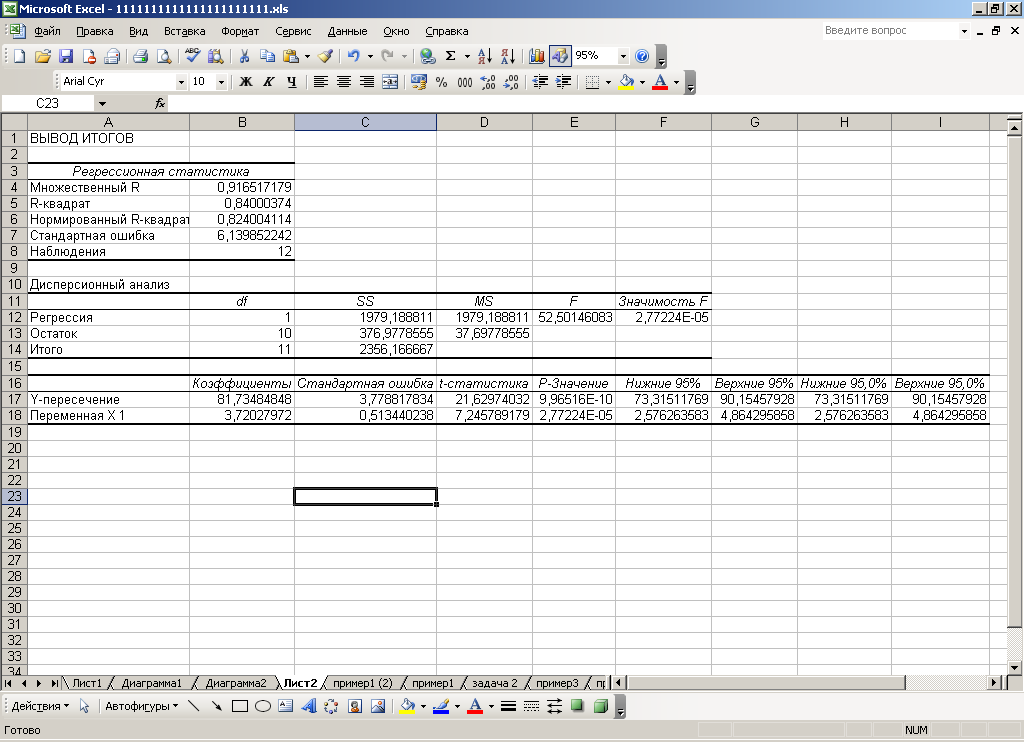
Рис. 3.5. Результати розрахунків регресійно-кореляційного аналізу

На рис. 3.6. представлена діаграма, на якій зображено обсяг реалізації товарної продукції, побудована ліня тренду та прогноз на чотири квартали.

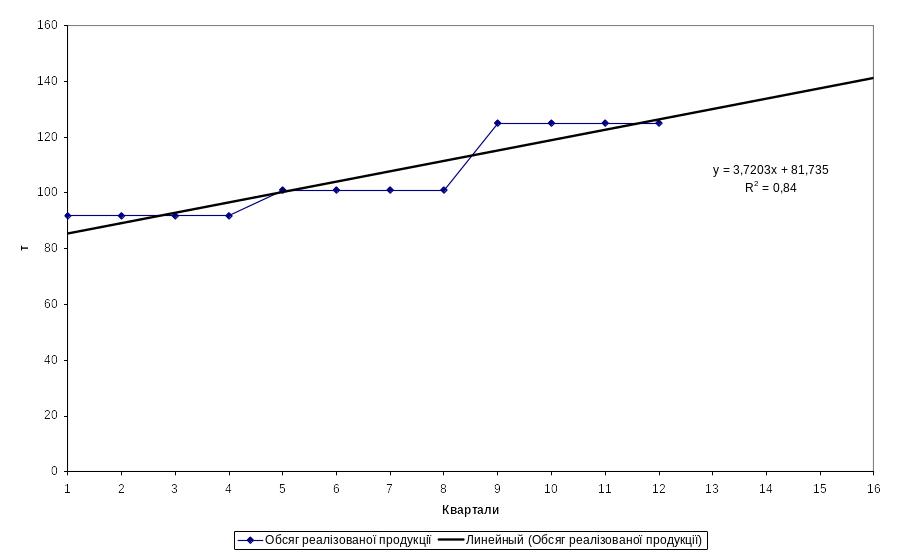
Рис. 3.6. Обсяг реалізації товарної продукції, побудована ліня тренду та прогноз на чотири квартали

Використовуючи побудовану модель а саме Y= 3,7203x + 81,735 визначимо прогнозні значення обсягу реалізації товарної продукції на чотири квартали.

Прогнозні значення обсягу реалізації товарної продукції представлені в табл. 3.4.

Таблиця 3.4