Некоторые свойства графов

М

h

a c d e b

f g k

j

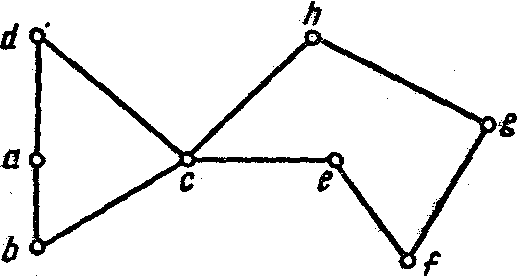
Рис 4.4 Граф, для которого мы отыскиваем последовательность вершин от а до b

аршруты

М аршрутом называется путь, проходящий от одной вершины к другой через ребра и вершины графа. Правильнее было бы опре­делить маршрут как последовательность ребер, образующую не­прерывный путь от исходной до конечной вершины. Если граф представляет файл или список, то последовательность ребер является поисковой последовательностью. С ее помощью можно осуществить поиск требуемой записи, анализируя записи в ячейках. Очевидно, эффективность поиска зависит от:

• структуры файла или списка его графа; • метода поиска — выбора последовательности ребер

На рис. 4.4 изображен граф с несколькими вершинами и ребрами.

Рассмотреть несколько последовательностей ребер. Самая прямая из них — acdeb. Поскольку здесь возможны ва­рианты, определим принцип их классификации. Будем считать, что последовательность ребер:

• элементарная, если в ней ни одно ребро или вершина не появляется более одного раза, например acdeb;

• простая, если в ней ни одно ребро не появляется более одного раза, например acdgjkgeb;

• непростая в остальных случаях.

Цикл

Последовательность ребер, в которой исходная и конечная вершины совпадают, называется циклом. Если последователь­ность ребер включает циклы, она не может быть элементарной. На рис, 4.5, например, последовательность gjkg является циклом, так как она берет начало и заканчивается в одной точке g.

Последовательность ребер acdgjkgeb содержит цикл gjkg. Эта последовательность является простой, так как в ней не повторя­ются ребра, но она не элементарная, так как вершина g по­является дважды.

По аналогии с последовательностью ребер можно провести классификацию циклов, разделяя их на элементарные, простые и т. д., причем к ним применимы те же определения. Воспользовавшись в качестве иллюстрации рис. 4.5, определим цикл как

• элементарный, если никакие вершины или ребра не появля­ются в нем больше одного раза, например abcda (хотя начальная и конечная вершины совпадают);

• п ростой, если никакое ребро не появляется более одного раза, например abcefghcda;

• непростой во всех остальных случаях, например, abcefghcba.

Рис 4.5 Изображение нескольких типов циклов

Маршруты орграфа

М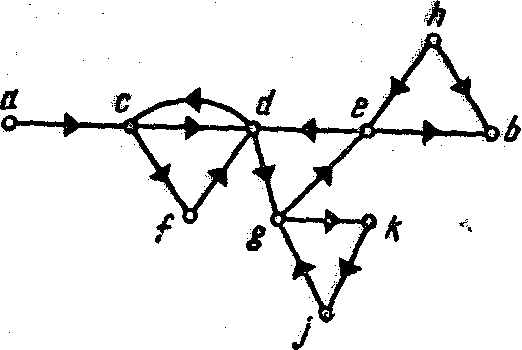 ногие структуры используют асимметричные отношения и поэтому представляются орграфами. Маршруты между различными точками орграфа называются последовательностями или цепочками дуг. Граф представляет собой удобный аппарат для передачи действий, выполняемых над такими структурами данных.

Рис 4.6 Орграф

На рис. 4.6 изображен орграф. Здесь также существует несколько последовательностей дуг между вершинами а и b. При определении таких последовательностей важно установить направление дуги. Мы можем перемещаться по дуге только в соответствии с указанием стрелки. Так, на рис. 4.6 acdgeb — элементарная последовательность дуг от а до b. Последовательность же acdeb является недопустимой, так как дуги de не существует, а есть только дуга ed.

Последовательности дуг также можно делить на: элементарные, простые и непростые, в зависимости от того, повторяется ли в них вершина или ребро.

Петли. В орграфе петли эквивалентны циклу. Петлей называется последовательность, начало и конец которой совпадают. Как и ранее мы должны помнить, что каждая дуга имеет свое направление. Петля считается определенной лишь тогда, когда из начальной точки, пройдя через различные промежуточные вершины в указанном стрелками направлении, возвратимся в исходную позицию. На рис. 4.7 показаны петли, отображающие циклы рис.4.6. Орграфы могут содержать цикл определяемые после удаления направленности из графа.

Из четырех циклов, представленных на рис. 4.7, только три являются петлями. Действительно, вершину h можно покинуть двумя путями, но нет пути, по которому можно было бы в нее вернуться.

Рис 4.7 Петли и циклы оргграфа, изображенного на рис 4.6

Петли также делятся на элементарные, простые и непростые, в зависимости от того, сколько раз встречается в них вершина или дуга.

Концепция петли, введенная теорией графов, сравнима с понятием “петли” или цикла используемым программистом. Очевидно, команды в программе можно рассматривать как вершины графа.

Дуги, которые соединяют команды, определяют последовательность, в которой ЭВМ переходит от одной команды к другой.

Геометрия

Граф представляет собой геометрическую фигуру, но принципы, которыми мы руководствуемся при его построении, отличаются от используемых в геометрии. Он не рассмат-

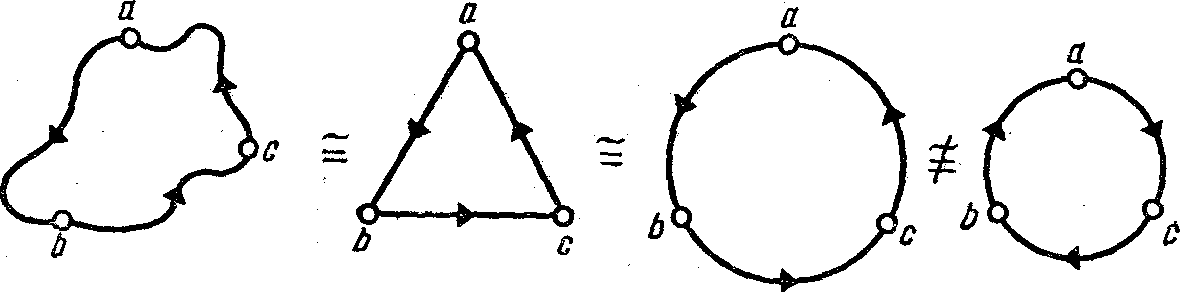
Рис. 4.8. Изоморфные орграфы

ривается в виде жесткой конструкции в своей плоскости. Более того, отрезки, сое­диняющие вершины, не обязательно должны быть прямыми.

На рис. 4.8 первые три орграфа графически эквива­лентны: каждый содержит три вершины и три соединяющие их, в одной и той же последовательности дуги. Их эквивалентность не зависит от того, как изображены дуги - прямыми, круговыми или волнистыми линиями. Третий и четвертый орграфы состоящие из трех дуг и трех вершин , не являются эквивалентными по теории графов. Дело в том, что в одном из них можно про­двигаться по петле в обратную сторону, а в другом нельзя.