20. Первое и второе достаточные условия экстремума.

4.Первое и второе достаточные условия существования экстремума функции в точке.

Первое достаточное условие:

Если непрерывная функция   дифференцируема в некоторой -окрестности критической точки   и при переходе через нее (слева направо) производная   меняет знак с плюса на минус, то  есть точка максимума; с минуса на плюс - то   есть точка минимума.

Доказательство:

Рассмотрим -окрестность точки  . Пусть   и  . Тогда функция   возрастает на интервале  , а на интервале   она убывает. Отсюда следует, что значение   в точке   является наибольшим на интервале  , т.е.   для всех  . Следовательно   есть точка максимума.

Второе достаточное условие:

Если в точке   первая производная функции   равна нулю ( ), а вторая производная в точке  ( ), то при   в точке   функция имеет максимум, а при   – минимум.

Доказательство:

Пусть  . Т.к.  , то   в достаточно малой окрестности точки  . Если  , то  , если  , то . Из этого следует, что при переходе через точку   первая производная меняет знак с минуса на плюс. Следовательно   есть точка минимума.

21. Выпуклая функция. Критерий выпуклости. Точка перегиба функции. Критерий чуществования точки перегиба.

Определение. Пусть   – промежуток,  :  . Функция   называется выпуклой, если всякий отрезок, соединяющий две произвольные точки графика функции  , лежит не ниже дуги графика функции  , соединяющей эти точки.

Теорема (критерий выпуклости для дифференцируемых функций). Пусть  ,   – промежуток, функция   дифференцируема. Функция   является выпуклой тогда и только тогда, когда функция   возрастает.

Доказательство. 

Так как   выпукла, то выполняется неравенство (2). Перейдем к пределу в этом неравенстве сначала при  , а затем при  . По теореме о предельном переходе в неравенствах имеем

  , значит,   возрастает.

Возьмем любые  . Применим теорему Лагранжа к функции   на промежутке  , а затем на  :

Так как   возрастает, то   

Отсюда следует, что   выпукла.

Точка перегиба функции   внутренняя точка   области определения  , такая что   непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и   является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки  , имеет в   точку перегиба, то  .Достаточное условие существования точки перегиба: если функция   в некоторой окрестности точки    раз непрерывно дифференцируема, причем   нечётно и  , и   при  , а  , то функция   имеет в   точку перегиба.

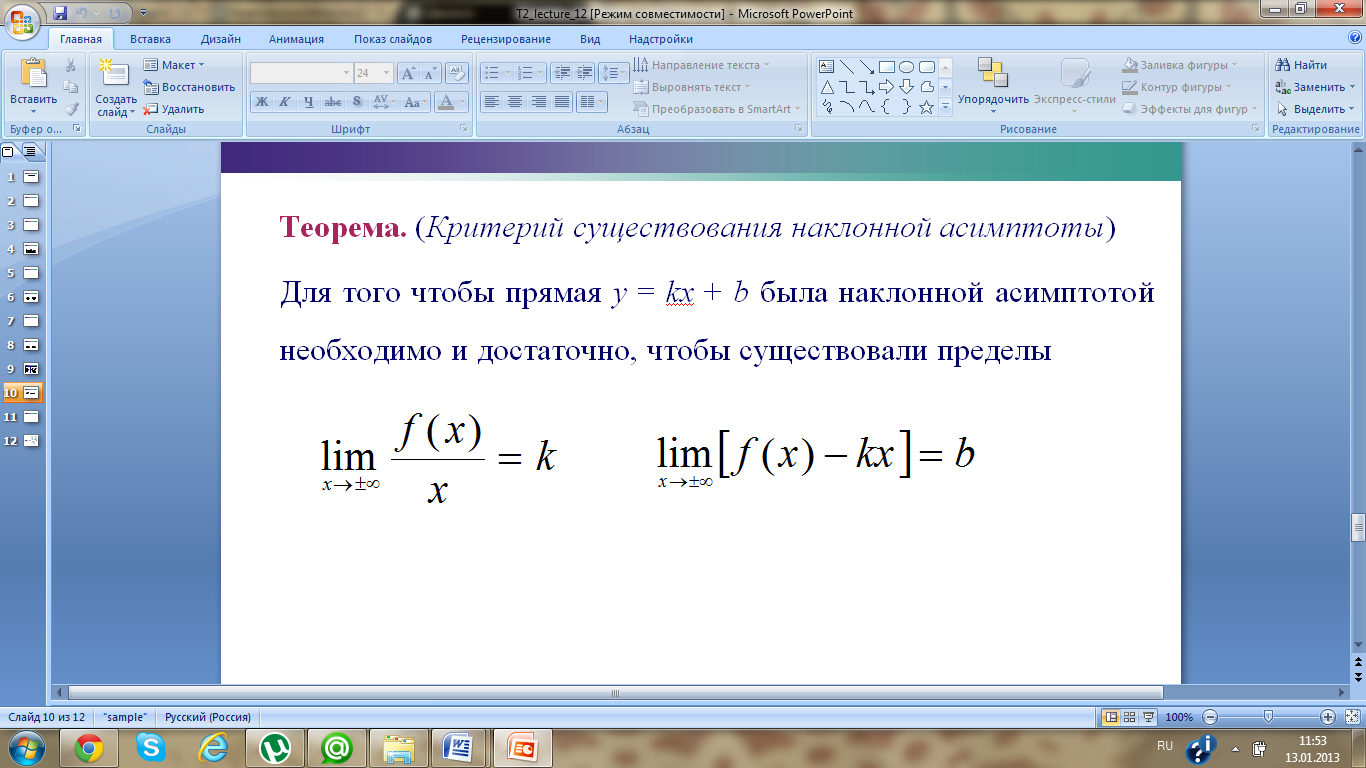
22. Асимптоты кривой. Теорема существования наклонной асимптоты.

Определение 9. Прямая L называется асимптотой кривой, если при движении точкиP по кривой в бесконечность, т.е. при  , окажется, что расстояние от точки P до прямой L стремится к нулю.

На рис. 6, 7 и 8 приведены примеры асимптот.

Асимптоты могут быть наклонными и вертикальными, горизонтальными.

Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий

,

Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если 

Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если   Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.

Для того чтобы прямая y = kx + b была наклонной асимптотой необходимо и достаточно, чтобы существовали пределы