18. Достаточное условие возрастания (убывания) функции непрерывной на отрезке.

1. Достаточное условие возрастания и убывания функции.

Теорема. 1) Если функция f(x), имеющая производную на отрезке [a, b], возрастает на этом отрезке, то ее производная на отрезке [a, b] не отрицательна, т. e. f' (x) ≥ 0.

2) Если функция f(x) непрерывна на отрезке [а, b] и диффе­ренцируема в промежутке (a, b), причём f' (x) > 0 для a < x < b, то эта функция возрастает на отрезке [а, b].

Доказательство. Докажем сначала первую часть теоремы. Пусть f(x) возрастает на отрезке [a, b]. Придадим аргументу x при­ращение : и рассмотрим отношение .

Так как f(x) — функция возрастающая, то при и при .

В обоих случаях , а следовательно, , т. е. f’(x)≥0, что и требовалось доказать. (Если бы было f' (x)< 0, то при достаточно малых значениях : отношение (1) было бы от­рицательным, что противоречит соотношению (2).)

Докажем теперь вторую часть теоремы. Пусть f ' (x) > 0 при всех значениях x, принадлежащих промежутку (a, b).

Рассмотрим два любых значения х₁ и х₂, х₁ < х₂, принадлежащих отрезку [a, b].

По теореме Лагранжа о конечных приращениях имеем:

По условию f’( )>0, следовательно, f(x₂)-f(x₁)>0, а это и значит, что f(x) - возрастающая функция.

Аналогичная теорема имеет место и для убывающей (дифференцируемой) функции, а именно.

Если f(x) убывает на отрезке [a,b], то f(x)^,0 на этом отрезке. Если f(x)<0 в промежутке (a, b), то f(x) убывает

на отрезке [a, b]. (Конечно, мы и здесь предполагаем, что функция непрерывна во всех точках отрезка [a, b] и дифференцируема всюду на (a, b).)

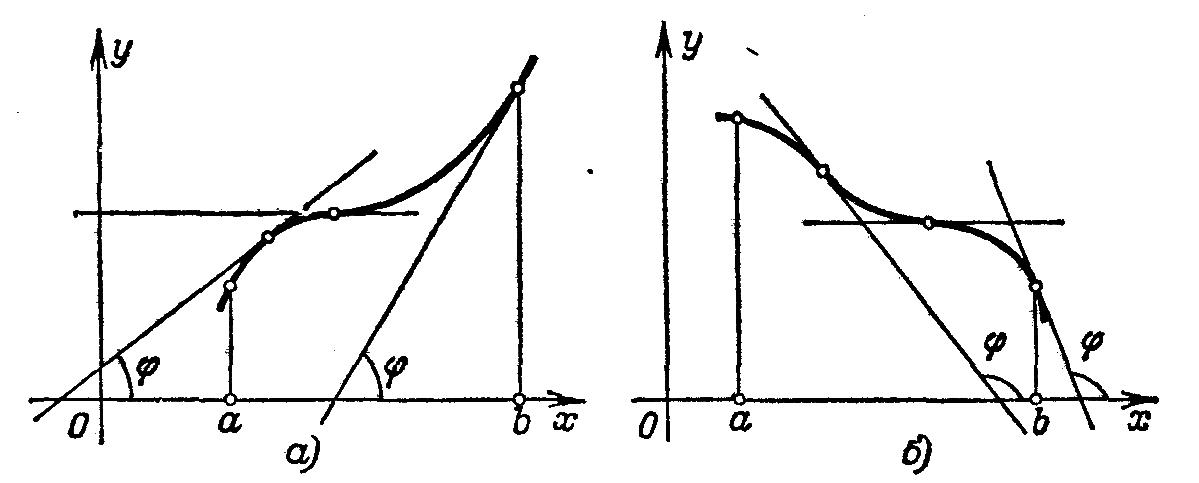
3aмeчaниe. Доказанная теорема выражает следующий геометри­ческий факт. Е сли на отрезке [a, b] функция f(x) возрастает, то касательная к кривой y=f(x) в каждой точке на этом отрезке об­разует c осью Ох оcтpый угол φ или - в отдельных точках - горизонтальна; тангенс этого угла не отрицателен: f’(x)=tgφ≥0 (рис. а). Если функция f(x) убывает на отрезке [a, b], то угол наклона касательной - тупой (или - в отдельных точках - ка­сательная горизонтальна); тангенс этого угла не положителен (рис. 6). Аналогично иллюстрируется и вторая часть теоремы. Теорема позволяет судить о возрастании или убывании функции по знаку ее производной.

19. Точки локального экстремума. Необходимое условие экстремума(теорема Ферма)

Пусть функция   определена в некоторой окрестности  ,  , некоторой точки   своей области определения. Точка   называется точкой локального максимума, если в некоторой такой окрестности   выполняется неравенство   (  ), и точкой локального минимума, если    .     

Теорема 1 (необходимое условие существования экстpeмума). Если дифференци­руемая функция y=f(x) имеет в точке x = х₂ максимум или мини­мум, то ее производная обращается в нуль в этой точке, т. e. f' (х₂) = 0.

Доказатeльcтво. Предпо­ложим для определенности, что в точке x=x₁ функция имеет максимум. Тогда при достаточно ма­лых по абсолютному значению приращениях Δx(Δx≠0) имеет место т. е. .

Но в таком случае знак отношения определяется знаком , а именно: при <0, при >0

Согласно определению производной имеем: .

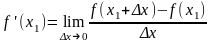Е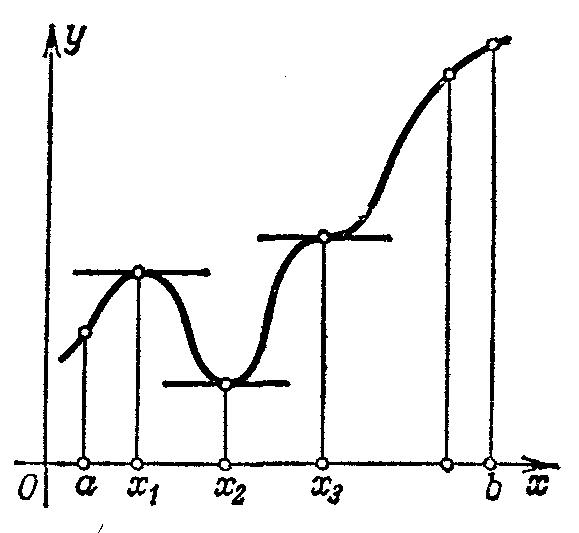 сли f(x) имеет производную при x = x₁ то предел, стоящий справа, не зависит от того, как : стремится к нулю (оставаясь положительным или отрицательным).

Но если →0, оставаясь отрицательным, то .

Если же →0, оставаясь положительным, то .

Так как f'(x₁) есть определенное число, не зависящее от способа стремления к нулю, то два последних неравенства совместимы только в том случае, если .

Аналогичным образом теорема доказывается и для случая мини­мума функции.