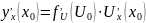12. Производная функции. Геометрический смысл производной. Касательная к плоской кривой.

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.

Определение 

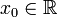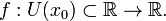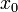1. Пусть в некоторой окрестности точки   определена функция  Производной функции   в точке   называется предел, если он существует,

• Производная функции в точке   обозначается символами

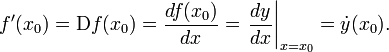
Дифференцируемость

Производная   функции   в точке  , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция   является дифференцируемой в точке   тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в   функции   в окрестности   справедливо представление

 

Тангенс угла наклона касательной прямой(геометрический смысл)

Если функция   имеет конечную производную в точке  то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число  является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Касательная к плоской кривой.

 Пусть даны кривая y = f(x) и точка M (x₁ ; y₁) на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).    Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x₁ ; y₁) равен значению f '(x₁)производной y' = f '(x) при x = x₁/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде

y - y₁ = f '(x₁)(x - x₁)

13. Теорема о непрерывности функции, имеющей конечную производную.

Теорема: Если функции имеет конечную производную, то она непрерывна в этой точке.

Доказательство:

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ< x < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

14. Бесконечные и односторонние производные. Теорема о производной сложной функции.

Односторонние производные

Говорят. Что функция y=f(x) имеет в точке x₀ бесконечную производную, равную (случай бесконечности исключается)

 Графики функции будут иметь в этих случаях односторонние касательные.  Возможно, и во внутренней точке отрезка [a,b] пределы отношения    существуют при   и при  , но не равны между собой. Это означает, что функция не имеет производной в этой точке, однако полученные пределы и в этом случае называются односторонними производными справа и слева; для графика функции существуют только односторонние касательные, сама точка на графике в этом случае называется угловой.

Бесконечные производные.

Можно ввести также понятие бесконечной производной       (последний случай может иметь место, если, например,  а  ). Сорри ребят, больше не могу найти ничего 

Теорема о производной сложной функции.

Если U=U(x) имеет конечную производную в точке x₀ и y=f(U) имеет конечную производную в U₀=U(x₀) то сложная функция y=f(U(x)) имеет в т. x₀ производную, причем , справедливо правило