Билет №1.

Вопрос 1.

Случайный процесс. Определение. Классификация. Характеристика сечений. Разновидности СП.

Определение: случайным процессом (СП) называется функция двух переменных , где - время; - пространство элементарных событий (ПЭС).

При любом фиксированном СВ называется сечением СП в точке .

При фиксированном значении детерминированная функция определенная на называется реализацией СП .

Случайный процесс считается заданным (по Слуцкому), если задана его n-мерная плотность распределения вероятностей (ПРВ) сечений , где .

СП с n-мерной гауссовской ПРВ называется гауссовским.

СП у которого выполняется равенство , где называется стационарным в узком смысле.

- настоящее сечение СП; прошлое сечение СП, будущее сечение СП. СП у которого будущее сечение зависит от настоящего и не зависит от прошлого называется марковским СП (МСП)

- переходная ПРВ, - начальная одномерная ПРВ.

В случае дискретного МСП вместо переходной ПРВ используется переходная вероятность.

Теорема Пуассона. Если дискретная ПСП, то

- вероятность случайных событий в интервале (0,t).

Для ПСП справедливо: При (бесконечно малая) , ; . (Вероятность того, что за малый промежуток времени произ. есть величина бесконечно малая).

. Время является непрерывной СВ, а сам процесс дискретный.

МСП делится на ПСП и ВСМ.

Поток событий при n=0,1,2.. удовлетворяющий условию (1) называется простейшим пуассоновским потоком (ПСП).

Винеровским СВ (ВСП) называется СП , которое удовлетворяет условиями:

1. процесс с независимыми приращениями

2. при любых , приращения распределяются одинаково

3.

4. при ; , , .

Если b=1 то ВСП называется стационарным.

Точечный процесс – последовательность случайных точек , на оси времени. Каждому ТСП можно сопоставить СП , определяющий число точек в интервале (0,t). Примером является ПСП, его реализация – ступенчатая функция со скачками равными единице.

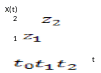
СВ характеризует расстояние между событиями, . Последовательность называется процессом восстановления.

Числовые характеристики.

Среднее значение (МО) СП: - для непрерывных СП; для дискретныйх СП.

Дисперсия СВ: - НСП; - ДСП.

Корелляционная функция:

Корелляционный момент:

Ковариационная функция (КВФ): =

Коэффициент корелляции: , сов

Взаимно корелляционные функции для двух процессов x(t) и y(t):

Корелляция между двумя значениями СП X(t) и Y(t) в два различных момента времени задается корелляционной матрицей:

Причем существенно свойство взаимной КФ: .

СП x(t) называется стационарным в широком смысле, если выполняются свойства:

1.

2.

3. для всех

3*.

В противном случае он называется нестационарным.

Эргодический СП.

Итак, пусть на интервале имеется среднее по времени:

очевидно, - случайная величина, причем ее среднее значение равно математическому ожиданию СП X(t):

Это значит, что СВ является несмещенной оценкой параметра .

Определение. Если выполняется условия и , то говорят, что СП X(t) эргодичен по среднему значению и пишут: