2.2. Рост по сложным и простым процентам

Для того чтобы сопоставить результаты наращения по разным процентным ставкам, достаточно сравнить соответствующие множители наращения. Нетрудно убедиться в том, что при одинаковых уровнях процентных ставок соотношения этих множителей существенно зависят от срока. Для того чтобы различать сложные и простые ставки, введем подписной индекс s для ставки простых процентов. Получим следующие соотношения множителей наращения:

для срока меньше года простые проценты больше сложных: (1 + ni_s) > (1 + i)ⁿ;

для срока больше года сложные проценты больше простых: (1 + ni_s) < (1 + i)ⁿ;

наконец, для срока, равного году, множители наращения равны друг другу при условии, что временная база для начисления процентов одна и та же.

Заметим также, что с увеличением срока (при n > 1) различие в последствиях применения простых и сложных процентов усиливается. Графическая иллюстрация соотношения множителей наращения приведена на рис. 2.3. В табл. 2.1 содержатся значения множителей наращения для i_s = i = 12%, K = 365 дней.

Таблица 2.1

Сравнение множителей наращения (i_s = i = 12%)

Множители наращения	Срок ссуды
	30 дней	180 дней	1 год	5 лет	10 лет	100 лет
1 + nis	1,01644	1,05918	1,12	1,6	2,2	13,0
(1 + i)n	1,00936	1,05748	1,12	1,76234	3,10584	83522,3

2.3. Наращение процентов т раз в году; номинальная и эффективная ставки

Номинальная ставка. В современных условиях проценты капитализируются обычно не один, а несколько раз в году — по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневное начисление процентов. При начислении процентов несколько раз в году можно воспользоваться формулой (2.1), однако параметр n в этих условиях будет означать число периодов начисления, а под ставкой i следует понимать ставку за соответствующий период. Например, при поквартальном начислении процентов за пять лет по квартальной (сложной) ставке 8% общее число периодов начисления составит 5 х 4 = 20. Множитель наращения равен 1,08²⁰ = 4,6609. На практике, как правило, в контрактах фиксируется не ставка за период, а годовая ставка и одновременно указывается период начисления процентов, например «18% годовых с поквартальным начислением процентов».

Итак, пусть годовая ставка равна у, а число периодов начисления в году равно т. Таким образом, каждый раз проценты начисляются по ставке j/m. Ставку j называют номинальной (nominal rate).

Формулу наращения теперь можно представить следующим образом:

S = P(1 + j/m)^N, (2.7)

где N — общее количество периодов начисления;

j — номинальная годовая ставка (десятичная дробь).

Если N — целое число (N = mn), то в большинстве случаев для определения величины множителя наращения можно воспользоваться таблицей сложных процентов (Приложение, табл. 2). Например, при j = 20% и поквартальном начислении процентов (т = 4) в течение пяти лет отыскиваем табличное значение множителя для i = 20/4 = 5% и п = 5 х 4 = 20; находим q = 2,653298.

Пример 2.7. Какова сумма долга через 25 месяцев, если его первоначальная величина 500 тыс. руб., проценты сложные, ставка — 20% годовых, начисление поквартальное?

По условиям задачи число периодов начисления N = 25:3 = 8 ¹/₃. Применим два метода наращения — общий и смешанный (см. формулу (2.4)). Соответственно получим

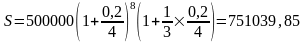руб.;

руб.

Эффективная ставка. Введем теперь новое понятие — действительная, или эффективная, ставка процента (effective rate). Эта ставка измеряет тот реальный относительный доход, который получают в целом за год от начисления процентов. Иначе говоря, эффективная ставка — это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m. Обозначим эффективную ставку через i. По определению множители наращения по двум видам ставок (эффективной и номинальной при m-разовом начислении) должны быть равны друг другу:

,

откуда

(2.8)

Как видим, эффективная ставка при т > 1 больше номинальной, при т = 1 i =j.

Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств участвующих сторон, т.е. обе ставки эквивалентны в финансовом отношении.

Пример 2.8. Какова эффективная ставка, если номинальная ставка равна 25% при помесячном начислении процентов?

i = (1 + 0,25/12)¹² - 1 = 0,280732.

Для сторон в сделке безразлично: применить ставку 25% (при помесячном начислении) или годовую ставку 28,0732%.

При подготовке контрактов может возникнуть необходимость и в решении обратной задачи — в определении j по заданным значениям i и т. Находим