А)Закон распределения дискретной случайной величины

Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.

Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения).

27. Вопрос 27.Математическое ожидание случайной величины, его свойства

А)Математическое ожидание случайной величины

Математическим ожиданием   дискретной случайной величины   называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *

Б)Свойства

1°. Математическое ожидание постоянной С равно этой постоянной.     Доказательство. Постоянную C можно рассматривать как случайную величину  , которая может принимать только одно значение C c вероятностью равной единице. Поэтому       2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

  3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин

28.

А)Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается 

Б)Свойства дисперсии

• Дисперсия любой случайной величины неотрицательна: 

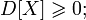
• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

• Если случайная величина равна константе, то её дисперсия равна нулю: 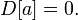  Верно и обратное: если 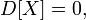  то 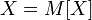  почти всюду;

• Дисперсия суммы двух случайных величин равна:

, где   — их ковариация;

• Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

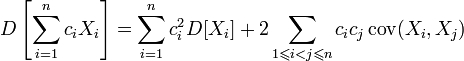, где  ;

• 

• 

• 

29. Вопрос 29. Испытания Бернулли. Биномиальное распределение

А)Испытания Бернулли - независимые испытания с двумя исходами каждое ("успехом" и "неудачей") и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей.

Б) Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна  .

30. Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

31. Функцией распределения вероятностей называют функцию  , определяющую вероятность того, что случайная величина   в результате испытания примет значение, меньшее  , то есть: . Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

32. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ

общее название Класса распределений вероятностей, возникающего при распространении идеи "равновозможности исходов" на непрерывный случай. Подобно нормальному распределению Р. р. появляется в теории вероятностей как точное распределение в одних задачах и как предельное - в других.

Р. р. на отрезке числовой прямой (прямоугольное распределение). Р. р. на каком-либо отрезке [ а, b], а<b, - это распределений вероятностей, имеющее плотность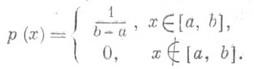 

Понятие Р. р. на [ а, b] соответствует представлению о случайном выборе точки на этом отрезке "наудачу". Математич. ожидание и дисперсия Р. р. равны, соответственно, (b+a)/2 и (b-а)²/12. Функция распределения задается формулой  .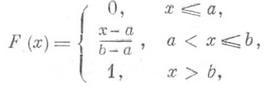

33. Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределением Гаусса —распределение вероятностей, которое задается функцией плотности распределения: где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривойплотности распределения, а σ² — дисперсия.

34. Локальная Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Р_п(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции 

где

 Интегральная теорема Муавра- Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Р_п(т₁, т₂) того, что событие А появится в п испытаниях от т₁ до т₂ раз. Приближенно равна определенному интегралу

   где

Данный интеграл называется функцией Лапласа и обозначается Ф(х).

• Ф(х)- нечетная функция

35. Функцией распределения случайного вектора   или совместным распределением случайных величин   называется функция, определенная равенством

,

где  .

 Говорят, что случайные величины  ,   имеют дискретное совместное распределение, если существует конечный или счётный набор чисел   такой, что

Таблицу, на пересечении  -й строки и  -го столбца которой стоит вероятность  , называют таблицей совместного распределения случайных величин   и  .

36. Ковариа́ция (корреляционный момент, ковариационный момент) в теории вероятностей и математической статистикемера линейной зависимости двух случайных величин. Пусть   — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

,

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле^[10][8]:

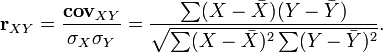
где  ,   — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы

37. Эмпирические: Пусть   — выборка объема   из неизвестного распределения   с функцией распределения  . Пусть   — эмпирическая функция распределения, построенная по этой выборке. Тогда для любого 

Теоритические???

38. То́чечная оце́нка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру. Пусть   — случайная выборка из распределения, зависящего от параметра  . Тогда статистику  , принимающую значения в  , называют точечной оценкой параметра