Вопрос 11.Определение и свойства неопределённого интеграла.
А)Неопределённый
интегра́л для
функции 
—
это совокупность всех первообразных данной
функции.
Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
Б)Свойства неопределенного интеграла
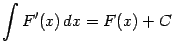
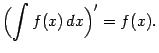
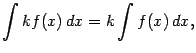
Таблица основных неопределённых интегралов
Слева
в каждом равенстве стоит произвольная
(но определённая) первообразная функция
для соответствующей подынтегральной
функции, справа же — одна определённая
первообразная, к которой ещё прибавляется
константа 
такая,
чтобы выполнялось равенство между
этими функциями.
Вопрос 12.Формула интегрирования по частям.
А)Формула интегрирования по частям
(u, v - дифференцируемые функции).
Б)По частям берутся интегралы следующих видов:
1) 
, 
, 
–
логарифм, логарифм, умноженный на
какой-нибудь многочлен.
2) 
,
–
экспоненциальная функция, умноженная
на какой-нибудь многочлен. Сюда же можно
отнести интегралы вроде 
–
показательная функция, умноженная на
многочлен, но на практике процентах
так в 97, под интегралом красуется
симпатичная буква «е».
3) 
, 
, 
–
тригонометрические функции, умноженные
на какой-нибудь многочлен.
4) 
, 
–
обратные тригонометрические функции
(«арки»), «арки», умноженные на какой-нибудь
многочлен.
Также по частям берутся некоторые дроби.
Пример:
1.
2.
3.
4. xLnx-x+C
Вопрос 13. Понятие (формула Ньютона-Лейбница) и свойства определённого интеграла.
А)Определенный интеграл – одно из основных понятий математического анализа – является мощным средством исследования в математике, физике, механике и других дисциплинах.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница.
Б)Формула Ньютона-Лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если 
непрерывна
на отрезке 
и 
—
ее любая первообразная на этом отрезке,
то имеет место равенство.
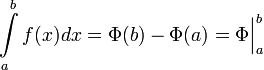
В)Свойства определенного интеграла
Условимся, что a < b.
1.Для
функции y
= f(x),
определенной при x
= a,
справедливо равенство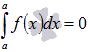 
.
2.
Для интегрируемой на отрезке [a;
b] функции
выполняется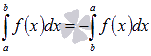 
.
3.
для
интегрируемых на отрезке [a;
b] функций y
= f(x) и y
= g(x).
4.
Постоянный множитель можно выносить
за знак определенного интеграла. То
есть, для интегрируемой на отрезке [a;
b] функции y
= f(x) и
произвольного числа k справедливо
равенство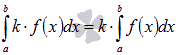
.
5.
Пусть функция y
= f(x) интегрируема
на интервале X,
причем 
и 
,
тогда 
.
6.
Если функция интегрируема на отрезке [a;
b],
то она интегрируема и на любом внутреннем
отрезке 
.
7.
Если функция y
= f(x) интегрируема
на отрезке [a;
b] и 
для
любого значения аргумента 
,
то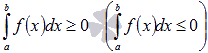 
.
8.
Пусть функция y
= f(x) интегрируема
на отрезке [a;
b],
тогда справедливо неравенство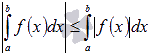 
.
9.
Пусть функции y
= f(x) и y
= g(x) интегрируемы
на отрезке [a;
b] и 
для
любого значения аргумента
,
тогда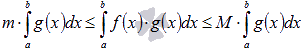 
,
где 
и 
.
10.
Первая формула среднего значения.
Пусть
функция y
= f(x) интегрируема
на отрезке [a;
b],
и
,
тогда существует такое число 
,
что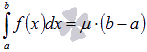 
.
11.
Вторая формула среднего значения.
Если
на отрезке [a;
b] функция y
= f(x) интегрируема,
а y
= g(x) монотонна,
то существует такое число 
,
что справедливо равенство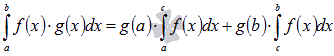 
.
Г) Этапы решения определенного интеграла следующие:
1)
Сначала находим первообразную
функцию 
(неопределенный
интеграл). Обратите внимание, что
константа 
в
определенном интеграле никогда
не добавляется.
Обозначение 
является
чисто техническим, и вертикальная
палочка не несет никакого математического
смысла, по сути – это просто отчёркивание.
Зачем нужна сама запись 
?
Подготовка для применения формулы
Ньютона-Лейбница.
2)
Подставляем значение верхнего предела
в первообразную функцию: 
.
3)
Подставляем значение нижнего предела
в первообразную функцию: 
.
4)
Рассчитываем (без ошибок!) разность 
,
то есть, находим число.
Готово.