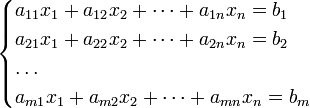Вопрос 5. Обратная матрица, способы ее нахождения.

А)Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Б)Способы нахождения обратной матрицы -

1.Сначала найдем определитель |A|

2,Находим матрицу миноров, путем вычеркивания столбца и строчки.

3. Находим матрицу алгебраических дополнений  .(Поменять знаки у нескольких чисел) (по диагонали у 2х2 матрицы, и ромбиком у 3Х3.

4.Дальше по формуле.

Вопрос 6. Ранг матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

А)Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.  ранг матрицы равен максимальному числу ее линейно независимых столбцов. 

Ранг матрицы А обозначается через r(A).

Б) Элементарные преобразования

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

В)Нахождение ранга матрицы

Найти ранг матрицы

А=   

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

 

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

 

;

 

из третьей строки вычтем первую; получим матрицу

В =  ,

 

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

Проще говоря. Надо с помощью вышеуказанных преобразований, надо сделать так чтобы остались только нули и однёрки, и количество однерок и будет рангом матрицы.

Вопрос 7. Системы линейных уравнений, их матричная форма записи. Методы решения.

А)Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Б)Матричный способ записи.

, при методе Крамера.

при методе Гаусса

В)Методы решения систем линейных уравнений

– Решение системы линейных уравнений методом подстановки («школьный метод»). – Решение системы методом почленного сложения (вычитания) уравнений системы. – Решение системы по формулам Крамера. – Решение системы с помощью обратной матрицы. – Решение системы методом Гаусса.