31. Максимальный поток в сети. Основные понятия.

Поток определяет способ передачи некоторых объектов из 1 вершины графа в другую по его дугам (ориентированным ребрам). Вершина, из которой начинается перемещение – источник (S).

Вершина, в которой заканчивается перемещение – сток (t). Объекты перемещения из S в t называются единицами потока.

Количество единиц потока проходящих по дуге (x, y) называются потоком по дуге (f(x, y))

C(x, y) – пропускная способность дуги (max количество единиц, которое можно передать за единицу времени)

Поток из S в t называется стационарным, если его дуговые потоки остаются неизменными в каждую единицу времени.

Дивергенцией ф-ии f в x называется разность сумм ее значений на исходящих и входящих в вершину x дугах.

Разрезом графа называется такое разбиение множества вершиной графа В на 2 подмножества X и 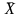, такое что, X принадлежит S, а - t.

Разрез сети с наименьшей пропускной способностью называется min разрезом.

Max поток в сети не может превышать пропускную способность min разреза в сети.

32.Алгоритм наращивания потока в сети

1. проанализировать граф и выделить допустимые дуги

2. составить из допустимых дуг увеличивающуюся цепь.

3. определить остаточную емкость цепи по формуле

4. увеличить поток в данной цепи. В прямых дугах величину потока увеличить на величину остаточной емкости. В обратных дугах – уменьшить.

5. повторять п.2-4 пока не останется ни одной увеличивающей цепи.

33. Раскраска графов. Хроматическое число

Граф g называется правильно раскрашенным λ красками, если каждая его вершина раскрашена одной из λ красок и никакие две смежные вершины не окрашены в 1 цвет. Если все эти условия выполняются, то говорят, что выполняется правильная раскраска графа λ красками.

Граф называется р-хроматичным, если существует правильная раскраска графа р-красками. Min из р – хроматическое число графа.

34 Алгоритмы раскраски графа

Определение независимого множества вершин

1) Выбирается произвольная начальная вершина и заносится в множество S

2) Выбирается вторая. Если эта вершина не смежна с S, то заносится в множество, иначе пропускается

3) Выполняется до тех пор, пока не будут просмотрены все вершины графа

Рекурсивная процедура

1) Выбрать в графе некоторое максимальное независимое множество вершин

2) Окрасить вершины данного множества в очередной цвет

3) Применять процедуру к оставшимся вершинам графа

По степеням вершин

1) Упорядочить вершины по степеням, начиная с максимальной

2) Задать начальное значение счетчика равное 1

3) Первую вершину окрашиваем в цвет k и заносим в букет

4) Если следующая вершина не смежна с вершинами букета, то окрашиваем ее в цвет k и добавляем в букет, иначе пропускаем

5) Проверяем количество просмотренных вершин. Если I меньше k, то возврат на действие, иначе k увеличивается на 1 и просмотр списка начинается заново, исключая окрашенные вершины. Если неокрашенных вершин не осталось, то конец алгоритма.

35. Логическая функция – это функция логических переменных, которая может принимать только два значения 0 или 1. В свою очередь сама логическая переменная тоже может принимать только два значения.

Способы задания ЛФ:

1. Словесная форма

2. Таблица истинности

3. Числовая форма

4. Карта Карно

5. В форме логического выражения

6. Геометрическая форма