26.Минимальное покрывающее дерево.

Алгоритм:

1.по матрице смежности отыскивают ребро с минимальным весом, отмечают «+». А его концевые вершины включают в 1ый букет.

2.Среди непросмотренных ребер выбирают ребро с минимальным весом и поступают с ним след. образом:

а) если его концевые вершины принадлежат одному и тому же букету, то его помечают знаком «-»;

б) если одна вершина принадлежит одному букету, а другая вершина не принадлежит ни какому другому букету, то 2ую вершину добавляем в

этот же букет, а эту вершину помечаем знаком «+»;

в) если ни одна из концевых вершин ребра не принадлежит ни одному из букетов, то эти вершины вкл. в новый букет, а ребро помечают знаком «+»;

г) если одна вершина принадлежит этому букету, а другая – другому, то букеты объедин. в один, а ребро помечают «+»;

3. выполняем пункт 2 до тех пор, пока все вершины не войдут в 1 букет.

28.Определение кратчайших путей в графе методом Форда-Белмана

Алгоритм:

1.начальной вершине S присваиваем значение 0, всем остальным вершинам – вес равный ∞

2.вершинам смежным начальным присваиваем вес инцидентных им ребер

3.на данном и послед. этапах определяем веса вершин, смежных с теми вершинами, которые изменили свой вес на предыдущем шаге по выражению

L′(v)= min (L(v); L(u)+a(u, v)))

4.определение кратчайших расстояний заканчивается на том шаге, когда ни одна из вершин не изменит своего веса.

В результате выполнения алгоритма веса вершин будут являться кратчайшими расстояниями от начальной вершине к этим вершинам. Сами же кратчайшие пути находятся по правилу: начин. с конечной вершины t определяются ребра, сост. кратчайший путь. Ребро принадлежит кратчайшему пути, если его вес равен разности весов инцидентных ему вершин, при этом из веса последующего пути вычитывается вес предыдущего.

29.Определение кратчайших путей в графе методом Дейкстры.

Алгоритм:

1.начальной вершине присваиваем вес равный 0, все остальным – равный ∞.

2.из полученных расстояний выбираем наименьшее ( в качестве постоянного наименьшего расстояния) Вершина соответствующая этому расстоянию – «определенная»

3.определяем новые расстояния к вершинам смежным с определенными по выражению

L′(v)= min (L(v); L(u)+a(u, v)))

4.определенная вершина удаляется из списка вершин к которым еще не определено расстояние

5.повторяем пункт 2-4 до тех пор, пока не станут определены все вершины графа, либо заданная конечная вершина T.

30. Определение кратчайших путей в графе методом Флойда-Уоршолла.

Алгоритм:

1.S=0

2. ,

3. к=1

4.рассматриваем К-тый столбец матрицы и в множество Ai выписываем номера элементов столбца ≠0 и ∞

5.рассматриваем К-тую строку матрицы и в множество Aj выписываем номера элементов строки ≠0 и ∞ (имеется в виду 0 по главной диагонали)

6.составляем декартово произведение Ai*Aj

7. для пар полученных в декартовом произведении рассчитываются новые значения в множестве

8.есл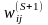и < , то вносятся изменения в матрицу путей =

9.значение счетчика S=S+1, w^(S+1), z^(S+1)

10.проверяется значение счетчика к, если к>h => k=k+1 и переход к пункту 4, иначе проверяется вносились ли изменения в матрицу w^(S), z^(s) во время изменения значения k от 1 до n. Если изменения не вносились, то конец алгоритма, иначе следовать к пункту 3.