16.Сочетания:

r – сочетания из n элементов без повторений:

r – сочетания из n элементов с неограниченным числом повторений:Место для формулы.

f(n,r)=C(n+r-1,r)

17.Разбиения. Набор целых положительных чисел п_1, п₂, ...,n_к называется разбиением числа п, если п = п₁ + п₂ + … + п_к. Числа п_i (i= 1, 2, …,k) называют частями, а их сумму n — ха­рактеристикой разбиения. При подсчете числа возможных разбие­ний могут учитываться дополни­тельные условия — тип разбие­ния, величины и общее число ча­стей, число повторений. Так, для числа 4 имеется 5 разбиений без ограничений (4, 31, 22, 211, 1111) и восемь разбиений с учетом поряд­ка частей (4,31,13, 22, 211, 121, 112, 1111). Число 8 разбивается на три части пятью способами: 611, 521, 431, 422, 332. Если принять в качестве производящей функции для разбиения числа п без ограничений р(п) многочлен р(х) – р(0) + p(1) х + р(2)х² + ..., определяется множителем (1 + )и, следовательно имеем:

p(x)=(1+x+

Из этого соотношения получаем производящие функции при ограничениях, накладываемых на численные значения частей. Если все части разбиения не превосходят числа k, то

Для разбиений, все части которых различны, имеем u(x)=(1+x)(1+ , а разбиения на нечетные части перечисляются функцией

18.Бином Ньютона.

Поставим соответствие каждому объекту из множества 1+α_ix, и перемножим их: (1)

Коэффициент a_r многочлена (1) представляет собой сумму произведений каждое из которых

образовано r – элементами из n. Если предположить что , то получим:

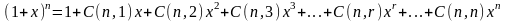(2)

Выражение (2) – Бином Ньютона коэффициенты перед х биномиальные коэффициенты с их помощью определяют количество сочетаний из n элементов длиной от 1 до n элементов также можно вывести формулы для сочетаний.

19.Полиномиальные производящие функции:

Используют для определения количества сочетаний с повторением элементов задаваемые с помощью спецификации вида: используются функции вида:

Если в спецификации указано строгое вхождение некоторого элемента то функция примет вид:

20.Экспоненциальные производящие функции:

Используются для определения количества перестановок с повторением элементов:

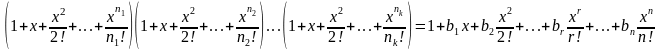
21.Метод включений и исключений:

Пусть имеется n объектов каждый из которых обладает свойствами N

Обозначим через N(α_i) – количество объектов которые обладают свойством α_i

Через N(α_i, α_j) 2-мя свойствами, N(α_i, α_j, α_k) 3-мя свойствами. Подчеркнём используемые объекты не обладающие свойствами

Число объектов не обладающих свойствами объединим формулами включения и исключения:

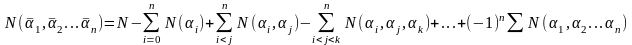
22.Основные понятия и определения теории графов.

Граф G(V,E) – совокупность 2-х множеств элементы которых называются вершинами V, и рёбрами Е. каждому ребру соответствует вершина.

Орграф – граф содержащий только ориентированные рёбра.

- Два ребра кратные инцидентны одной и той же паре вершин.

- Ребро графа называется петлёй если оно инцидентно одной вершине.

- Граф не содержащий кратных рёбер и петель называется простым.

- Граф содержащий кратные рёбра называется мультиграфом

- Под графом графа G называется граф у которого все вершины и рёбра принадлежат графу G.

- Оставным подграфом называется граф содержащий все вершины графа G.

- Граф лонарный(плоский) если он может быть изображён на плоскости так что его рёбра пересекаются только в вершинах.

- Степенью вершины p(v) называется число инцидентных ей рёбер и дуг.

- Полустепенью захода p⁺(v) называется число входящих рёбер в вершину.

- Полустепенью исхода p^-(v) называется число исходящих рёбер из вершины.

- Вершина 1-й степени называется висячей, а 0-й степени изолированной.

- Сетью называется граф G(V,E,F) который рассматривается вместе с функцией F приписывая каждому ребру принадлежащему Е число(вес ребра F(e)).

-Маршрутом в графе G называется последовательность чередующихся вершин и рёбер, что каждое ребро последовательно инцидентно двум вершинам одна предшествует ему, а другая следует за ним.

- Маршрут называется цепью - если его рёбра различны, простой цепью если и вершины различны замкнутая цепь – цикл.

- Путём называется цепь направление дуг в которой совпадает.

- Связный граф – граф в котором хотя бы две вершины соединены цепью.

- Дерево - Связный граф без циклов.

- Эйлеровый цикл – такой цикл в графе который обходит каждое ребро графа в точности один раз.

- Гоментонов цикл – цикл обходящий один раз каждую вершину.

23.Способы задания графов:

1.Матрица смежности

2.Матрица инцидентности

3.Список пар вершин

4.Список смежности

24.Определение связности графа методом поиска в глубину:

Алгоритм:

1.Начальную вершину S помещаем в стек

2.Определяем новую вершину смежную с S если такой нет то поиск окончен вершина S не связана с вершиной графа если же S смежна с вершиной v_i, то v_i помещаем в стек.

3.Определяем новую вершину смежную с последней вершиной помещённой в стек, если вершина есть то добавляем её в стек и повторяем (3), иначе её перемещаем в СИВ, а поиск продолжаем из крайней вершины стека.

4.Выполняем пункт (3)до тех пор пока из стека в СИВ не перейдёт начальная вершина S.

25.Определение связности графа методом поиска в ширину.

Алгоритм:

1.Начальную вершину S помещаем в очередь определённые новые вершины смежные с S если нет, то поиск окончен вершина S несвязанна с другими вершинами графа, если же S смежна в вершине.

2. v_i… v_j , то эти вершины новые после чего вместе с S перемещаем в СИВ.

3.Из СИВ выбираем следующую вершину за v_i и помещаем в очередь, определяем смежные с ней новые вершины и помещаем в список новых и использованных вершин.

Если новых нет то (4).

4.В очередь помещается следующая вершина из СИВ для которой выполняется действие пункта (3).

5.Поиск заканчивается тогда когда в очереди просматривается все вершины из СИВ.

26. Метод построения дерева путей.

Алгоритм:

1.Корню дерева путей образованного вершиной S присваиваем 0-й уровень.

2.Из корня дерева строятся ветви 1-го уровня на концах которых помещаются вершины 1-го уровня смежные с S.

3.Ветви 2-го уровня строят из вершины находятся на 1-м уровне при этом из вершины 1-го уровня выходит столько ветвей со сколькими вершинами графа смежна эта вершина исключая S.

4.Строятся ветви и вершины 3-го и далее аналогично пункту (3) при этом вершина может включаться в уровень если она ранее не встречалась.

5.Конец тогда когда будут охвачены все связи в графе.