1.Способы задания множеств:

1. Перечислением элементов А=(1,2,3,4,5,6)

2. Описанием элементов множества общим свойством Р(х), где Р(х) – высказывание или выражение.

2.Операции над множествами:

Объединение = «Все элементы множеств»

Пересечение = «Общие элементы множеств»

Разность = «Элементы первого которых нет во втором»

Дизъюнктивная сумма = «Различные элементы обоих множеств»

Декартово произведение = «Композиция»

3.Законы алгебры множеств:

1. Коммутативный закон: А∩В=В∩А; АUВ=ВUА;

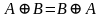
2. Ассоциативный закон: (А∩В)∩С=А∩(В∩С); (АUВ)UС=АU(ВUС);

3. Дистрибутивный закон: АU(В∩С)=(АUВ)∩(АUС); А∩ (ВUС)=(А∩В) U (А∩С)

4. Аксиомы алгебры множеств: ; ; ; ; ; ; ; ; .

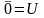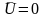5. Закон идемпотентности: АUАUАUАU……UA=A; A∩A∩A∩A∩……∩A=A

6. Закон поглощения: А∩ (АUВ)=А; АU(А∩В)=А

7. Закон де Моргана: ;

8. Раскрытие дизъюнктивной суммы:

4.Круги Эйлера: Используются для представления операций с множествами, а также для доказательства тождеств.

5.Функции и отображения- Всякое функциональное отношение можно рассматривать как функцию. При этом первая координата х упорядоченной пары (х_, у) А является аргументом (переменной), а вторая у — образом (значением) функции. Обычная запись у = f(x) соответствует соотношению xfy, или (х, у) f. Следует различать функцию f как множество упорядоченных пар (отноше­ние) и значение функции у = f(x) как вторую координату одной из таких пар.

Для всякого функционального отношения А можно определить связанную с этим отношением функцию f. Но симметричное к нему отношение может и не быть функцией. Так, отношение ={( , ),( ),( ( } обратное рассмотрен­ному в (1), не является функцией.

Если функциональное отношение Aподмножество X х Y всюду определено на X, т. е. его область определения D₀(A) совпадает с множеством X, то его называют отображением множества X в Y и записывают

Y

Отображение можно также рассматривать как функцию f, определенную на множестве X и принимающую значения в мно­жестве Y.

Как видно, различие между отображением и функцией сво­дится к способу определения этих отношений на множестве X, причем отображение следует рассматривать как частный случай функции. Однако большинство авторов не различают понятия ото­бражения и функции, оставляя открытым вопрос об области опре­деления. Если f — отображение или функция, то пишут f : X Y или проще х f(x).

6.Типы отображения

при отображении Х в У все элементы Х участвуют в отображении, но вовсе не обязательно чтобы в этом отображении участвовали все элементы из У.

а) если любой элемент у из множества У является образом хотя бы одного элемента х из Х, то такое отображение называется сюрьекцией

б) если для любых двух различных элементов х1 и х2 есть образы f(x1), f(x2) также различны, то такое отображение называется иньекцией.

в) отношение сюрьективно и иньективно называется биекцией.

7.Операции над отображениями

функция f определена на множестве Х, а функция f1 определена на множестве Q является подмножеством Х, причём для каждого Х значения f и f1 совпадают, тогда функцию f1 называют сужением функции f на множестве Q. В свою очередь f называют продолжением функции f1 на множестве Х.