20.Формула Тейлора

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.

Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Пусть функция бесконечно дифференцируема в некоторой окрестности точки . Формальный ряд

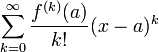
называется рядом Тейлора функции в точке .

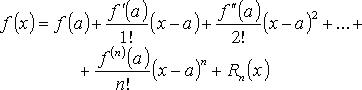
21.Условия возрастания и убывания функции.

Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Теорема 1

1. Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

2. Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].

Аналогичная теорема имеет место и для убывающих функций.

Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].

Теорема 1.

Дифференцируемая и возрастающая в интервале ( a, b ) функция f (x) имеет во всех точках этого интервала неотрицательную производную.

Теорема 2. Дифференцируемая и убывающая в интервале ( a, b ) функция f(x) имеет во всех точках этого интервала неположительную производную.

Теорема. Для того чтобы функция f (x), дифференцируемая в точке х₀ Î (а, b), возрастала (убывала) в точке x₀, необходимо, чтобы её производная в точке х₀ была неотрицательной f ' (x₀) ≥ 0 (неположительной f ' (x₀) ≤ 0). Теорема. Если функция f (x) определена на отрезке [а, b], дифференцируема в точках х Î (а, b) и

f ' (x) > 0, ( f ' (x) < 0),

то функция f (x) возрастает (убывает) на отрезке [а, b ].    Доказательство. Применим теорему о конечных приращениях для двух произвольных точек х₁ < х₂ Î [а, b]

f (x₂) − f (x₁) = f ' (c)·( x₂ − x₁),

где с Î ( x₁ ; x₂). Из этого соотношения следует

sign ( f (x₂ ) − f ( x₁ ) ) = sign f ' ( c)

   В случае f ' (x) > 0 для всех х Î (а, b) имеем f (x₂) > f (x₁) , и большему значению аргумента соответствует большее значение функции. Что свидетельствует о возрастании функции.

22.23.Экстремумы.Необходимые условия экстремума.

Экстремум— максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум). Дополним, что точки, где производная равна нулю, называются стационарными ; а точки, где производная не существует называются критическими.

1 Достаточное условие пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х₁, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х₁. Если при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то при х = х₁ функция имеет локальный максимум. Если же при переходе слева направо через эту точку х₁ производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.    Комментарий. Если в достаточно малой окрестности точки х₁ справедливо f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁, то в точке х₁ функция имеет максимум; если f ' (x) < 0 при х < x₁, f ' (x) > 0 при х > x₁, то в точке х₁ функция имеет минимум.

2.Необходимое условие Если х₀ — точка экстремума функции f (x), то либо в этой точке производная обращается в нуль f ' (x₀) = 0 (в стационарных точках), либо в этих точках производная не существует (в угловых точках).

Пусть функция определена в некоторой окрестности , , некоторой точки своей области определения. Точка называется точкой локального максимума, если в некоторой такой окрестности выполняется неравенство ( ), и точкой локального минимума, если .     

Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.

Следующая теорема даёт необходимое условие того, чтобы точка была точкой локального экстремума функции .