
- •2.Множество-набор элементов а.
- •Второй замечательный предел:
- •8.Свойства функций непрерывных на отрезке.
- •10.Необходимые и достаточные условия дифференцируемости. Дифференциал
- •11.Производная элементарных функций
- •12.Правила дифференцирования
- •13.Производная сложной и обратной функции. Логарифмическое дифференцирование.
- •14.Производная параметрически заданной функции и производная наявно заданной функции.
- •15.Производные и дифференциалы высших порядков.
- •16.Теорема Ролля
- •17.Теорема Лагранжа
- •18.Теорема Коши
- •19.Правило Лапеталя
- •20.Формула Тейлора
- •21.Условия возрастания и убывания функции.
- •25.Неопределенный интеграл. Таблица первообразных.
- •24.Выпуклость и вогнутость функции. Асимптоты.
- •26.Методы интегрирования.
- •27.Интегрирование рациональных функций
- •28.Интегрирование тригонометрических функций
- •29.Интегрирование иррациональных функций.
- •30.Определенный интеграл
- •31.Формула Ньютона-Лейбница.
- •32.Замена переменной и интегрирование по частям в опр. Интеграле.
- •33.Несобственный интеграл
- •34.Функции нескольких переменных
- •35.Предел функции двух переменных
- •37.Частные производные
- •38.Двойной интеграл
- •39.Экстремумы функции нескольких переменных.
17.Теорема Лагранжа
Формула конечных
приращений
или теорема
Лагра́нжа о среднем значении
утверждает, что если функция
непрерывна
на отрезке
и
дифференцируема в интервале
,
то найдётся такая точка
![]() ,
что
,
что
![]() .
.
Геометрически это можно переформулировать так: на отрезке найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое
истолкование:
Пусть
![]() —
расстояние точки в момент
—
расстояние точки в момент
![]() от
начального положения. Тогда
от
начального положения. Тогда
![]() есть
путь, пройденный с момента
есть
путь, пройденный с момента
![]() до
момента
до
момента
![]() ,
отношение
,
отношение
![]() —
средняя скорость за этот промежуток.
Значит, если скорость тела определена
в любой момент времени
—
средняя скорость за этот промежуток.
Значит, если скорость тела определена
в любой момент времени
![]() ,
то в некоторый момент она будет равна
своему среднему значению на этом
участке.
,
то в некоторый момент она будет равна
своему среднему значению на этом
участке.
Доказательство
Для функции одной переменной:
Введем функцию
![]() .
Для нее выполнены условия теоремы
Ролля: на концах отрезка ее значения
равны
.
Для нее выполнены условия теоремы
Ролля: на концах отрезка ее значения
равны
![]() .
Воспользовавшись упомянутой теоремой,
получим, что существует точка
.
Воспользовавшись упомянутой теоремой,
получим, что существует точка
![]() ,
в которой производная функции
,
в которой производная функции
![]() равна
нулю:
равна
нулю:
![]()
что и требовалось доказать.
18.Теорема Коши
Пусть даны две
функции
![]() и
и
![]() такие,
что:
такие,
что:
и определены и непрерывны на отрезке
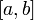 ;
;производные
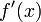 и
и
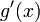 конечны
на интервале
конечны
на интервале
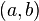 ;
;производные и не обращаются в нуль одновременно на интервале
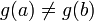 ;
;
тогда существует
![]() ,
для которой верно:
,
для которой верно:
![]() .
.
(Если убрать
условие 4, то необходимо, например,
усилить условие 3: g'(x) не должна обращаться
в нуль нигде в интервале
![]() .)
.)
Для доказательства введём функцию
|
|
Для неё выполнены
условия теоремы
Ролля:
на концах отрезка её значения равны
.
Воспользовавшись упомянутой теоремой,
получим, что существует точка
,
в которой производная функции
равна
нулю, а
![]() равна
как раз необходимому числу.
равна
как раз необходимому числу.
19.Правило Лапеталя
Условия:
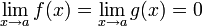 или
или
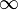 ;
;и
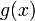 дифференцируемы
в проколотой окрестности
;
дифференцируемы
в проколотой окрестности
;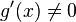 в
проколотой окрестности
;
в
проколотой окрестности
;существует
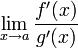 ,
,
тогда существует
![]() .
.
Пределы также могут быть односторонними.
Доказательство
Отношение
бесконечно малых: покажем
теорему для случая, когда пределы
функций равны нулю (то есть неопределённость
вида
![]() .
.
Поскольку мы
рассматриваем функции
и
только
в правой проколотой полуокрестности
точки
,
мы можем непрерывным
образом
их доопределить в этой точке: пусть
![]() .
Возьмём некоторый
из
рассматриваемой полуокрестности и
применим к отрезку
.
Возьмём некоторый
из
рассматриваемой полуокрестности и
применим к отрезку
![]() теорему
Коши.
По этой теореме получим:
теорему
Коши.
По этой теореме получим:
![]() ,
,
но
,
поэтому
![]() .
.
Отношение бесконечно больших:-
