14.Производная параметрически заданной функции и производная наявно заданной функции.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументу x, считая y – функцией от x, и после этого выразить .

Производная параметрически заданной функции

Если функция f задана параметрически

x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

Производная неявно заданной функции

Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения

15.Производные и дифференциалы высших порядков.

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,

f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))',   n ϵ N,   f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,

dⁿf(x) = d(d^n-1f(x)),   d⁰f(x) = f(x),   n ϵ N.

Если x - независимая переменная, то

dx = const   и   d²x = d³x = ... = dⁿx = 0.

В этом случае справедлива формула

dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

16.Теорема Ролля

Если вещественная функция, непрерывная на отрезке и дифференцируемая на интервале , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Теорема Ро́лля (теорема о нуле производной)

Доказательство. Рассмотрим два случая.

1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.

2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.

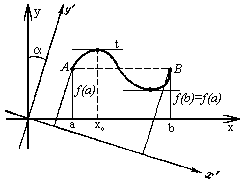
Рис.1

Пусть например f(x0) - наибольшее значение функции f(x) на интервале [а, b] и x0 - внутренняя точка этого интервала. Тогда f(x0) является максимумом функции: f(x0) і f(x) для всех x из достаточно малой окрестности x0 [за эту окрестность можно впрочем, взять интервал (а, b)].

Так как, по условию, f(x) имеет в точке x0 производную, то по теореме о необходимом признаке экстремума,

f ' (x0) = 0,

и теорема Ролля доказана.

Геометрический смысл

Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

Следствие

Если непрерывная функция обращается в ноль в различных точках, то ее производная обращается в ноль по крайней мере в различных точках^[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.