31.Формула Ньютона-Лейбница.

Вычисление определенного интеграла.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо равенство .

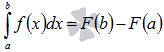Эту формулу называют основной формулой интегрального исчисления.

32.Замена переменной и интегрирование по частям в опр. Интеграле.

 Интегрирование по частям

или

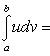
(u, v непрерывно дифференцируемы на интервале ).

  Замена переменного (интегрирование подстановкой)

     Если функция x = x(u) непрерывно дифференцируема на интервале , а функция f(x) непрерывна на интервале , где m - точная нижняя, а M - точная верхняя граница функции x(u) на интервале , то

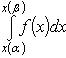
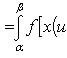
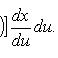
33.Несобственный интеграл

Пусть функция y = f(x) определена и интегрируема на произвольном отрезке [а, t], т.е. функция

определена для произвольного значения t ≥ a. Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел

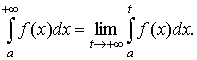(9.1)

   Если предел, стоящий в правой части равенства (9.1), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае — расходящимся.    Выделяют следующие две задачи: а) исследование вопроса о сходимости заданного несобственного интеграла; б) вычисление значения интеграла в случае, если несобственный интеграл сходится.

34.Функции нескольких переменных

Если каждой упорядоченной паре чисел по некоторому закону поставлено в соответствие единственное действительное число , то говорят, что задана функция двух переменных или . Числа называются при этом независимыми переменными или аргументами функции, а число – зависимой переменной.

Значение функции в точке обозначают или и называют частным значением функции двух переменных.

Совокупность всех точек , в которых определена функция , называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.

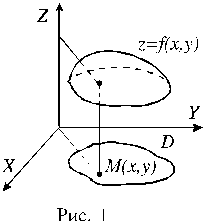
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)ÎD. График представляет собой некоторую поверхность. Пример такой

поверхности приводится на рисунке 1.

35.Предел функции двух переменных

Для того чтобы дать понятие предела функции нескольких переменных, ограничимся случаем двух переменных х и у. По определению функция f (x, y) имеет предел в точке (х0, у0), равный числу А, обозначаемый так:

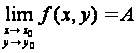(1)

(пишут еще f (x, y)→А при (x, y)→ (х0, у0)), если она определена в некоторой окрестности точки (х0, у0), за исключением, быть может, самой этой точки и если существует предел

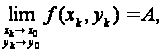(2)

какова бы ни была стремящаяся к (х0, у0) последовательность точек (xk, yk).

Число А называется пределом функции z=f(x,у) в точке М₀(х₀, у₀), если для каждого числа ε>0 найдется такое число β>0, что для всех точек М(х,у), для которых выполняется неравенство |ММ₀|<β, будет выполняться неравенство | f(x,у)– A|< ε      Обозначим .

36.Дифференцирование функции нескольких переменных. Дифференциал