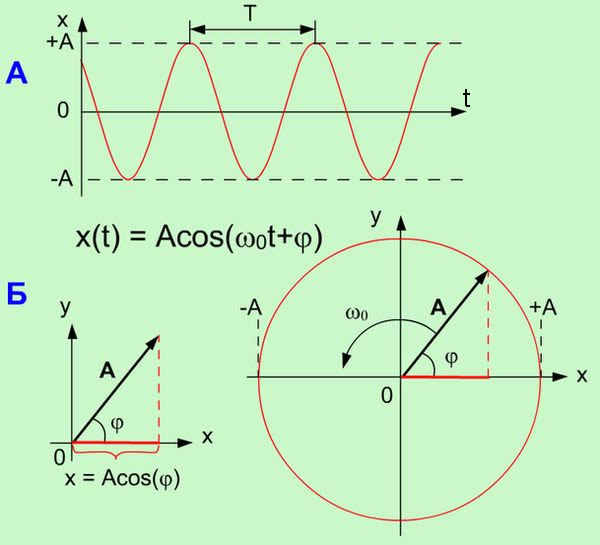
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид:
где A - амплитуда колебаний - величина наибольшего отклонения системы от положения равновесия.
- круговая
(циклическая) частота. Частота
гармонических колебаний
равна: ν = 1/T. Единица измерения частоты
герц (Гц) - одно колебание в секунду.
Круговая частота = 2π/T = 2πν дает число колебаний за 2π секунд.
Периодически
изменяющийся аргумент косинуса
- называется фазой
колебаний.
Фаза колебаний определяет смещение
колеблющейся величины от положения
равновесия в данный момент времени t.
Постоянная (фи) представляет собой
значение фазы в момент времени t = 0 и
называется
начальной фазой колебания.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Период гармонических колебаний равен: T = 2π/ .
Дифференциальное уравнение свободных затухающих колебаний
где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания, w0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
(Ангармонический осциллятор не нашёл)
Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени (колебания маятников, струн, балок, частей машин и механизмов, качка кораблей, волнение моря, колебания давления при распространении звука в газе, жидкости, твердом теле и т.д.).
Гармонический
осциллятор
(в классической механике) — это система,
которая при смещении из положения
равновесия испытывает действие
возвращающей силы F
, пропорциональной смещению x
(согласно закону Гука):
где k — положительная константа, описывающая жёсткость системы.
Если — F единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
законы движения математического и физического маятников
При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой ( ) смещений и , которые запишутся следующими выражениями:
Значения амплитуды А и начальной фазы (фи) этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз.
Если угол (разность
фаз: Δ(фи) = (φи)1 – (φи)2) между векторами
А1 и А2 равен 0, то исходные колебания
находятся в фазе
и суммарная амплитуда (А =А1 +А2) будет
максимальна. Если угол (разность фаз:
Δ(φи) = (φи)1 – (φи)2) между векторами А1 и
А2 равен - π или π, то исходные колебания
находятся в противофазе
и суммарная амплитуда (А =
А1
-А2
)
будет минимальна.
Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса.
За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π/Δω). Δω -разность круговых частот исходных колебаний.