1 VaR – мера риска 1

1.1 История VaR 1

1.2 Оценка позиции, подверженной риску (VaR) 1

2 Форвардный кредит 5

2.1 FRA 6

2.2 Фьючерс на евродепозит 8

2.3 Фьючерс на казначейские векселя 11

3 Своп 13

3.1 Простой процентный своп 13

3.2 Методы определения справедливой стоимости свопа 14

1. VaR – мера риска

VaR – это мера, предназначенная для оценки риска портфеля. Она рассчитывается на основе оценки риска по каждой позиции портфеля по отдельности. Затем эти отдельные риски собираются в агрегированный риск портфеля.

VaR – это суммарная, выраженная в одной цифре статистическая мера возможных потерь по портфелю. Более того, VaR – это мера возможных потерь в результате «нормального» движения рынка. Потери большие, чем VaR также могут случиться, но с очень маленькой вероятностью.

Отражение совокупного портфельного риска в виде одной цифры удобно:

1. для разработки нормативов подверженности риску,

2. для отчетов перед регулирующими органами,

3. для использования в корпоративной отчетности.

Оценка величины потерь будет зависеть от:

1. распределения вероятностей, которое характерно для имеющихся активов,

2. корреляции между активами портфеля, и

3. доверительного интервала, который устраивает менеджера.

Доверительный интервал определяется дизайнером системы, риск-менеджером. Например, J.P. Morgan в своем RiskMetrics использует 95% доверительный интервал.

Оценка величины возможных потерь обычно строится с помощью трех основных методов:

1. аналитического (метода вариации-ковариации);

2. имитационного моделирования:

   1. историческая имитация;

   2. имитация Монте-Карло.

1. История VaR

Value at risk стала использоваться крупными финансовыми институтами в начале 1980-х годов для измерения риска их портфелей.

2. Оценка позиции, подверженной риску (VaR)

Предположим, что немецкая фирма имеет в составе своего портфеля 30-дневный вексель Казначейства США в 500 тыс. долл. Если доллар будет расти, то фирма в выигрыше, если он будет падать, то, напротив, в проигрыше.

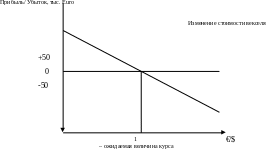
Рисунок 1. Зависимость прибыли/ убытка от курса

Этот график показывает зависимость, но не показывает, сколько мы можем потерять.

Берем временной ряд и оцениваем 30-дневную волатильность евро к доллару. Предположим, стандартное отклонение равно 0.0625 $/€. Предполагаем, что валютный курс приблизительно нормален.

μ = 0 (процентный темп роста равен нулю)

σ = 0.0625.

Выбираем нужный доверительный интервал (confidence interval). Доверительный интервал выражается в «сигмах»:

1. 1∙σ – 68%-й доверительный интервал

2. 1.28∙σ – 90%-й доверительный интервал

3. 1.64∙σ – 95%-й доверительный интервал

4. 2.33∙σ – 99%-й доверительный интервал

5. 3.1∙σ – 99.9%-й доверительный интервал

В сигмах интервалы считать неудобно, поэтому нужно перевести в денежные единицы.

VaR = k∙σ∙V

где

k – количество стандартных отклонений, соответствующих нужному доверительному интервалу. Например, для 95%-го доверительного интервала k=1.64.

σ – стандартное отклонение

V – позиция, подверженная риску (в нашем примере 500 тыс. долл.).

поскольку μ = 0, то

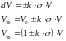
Для доверительного интервала 95% изменение позиции через 30 дней должно лежать в пределах:

где

V_u - верхнее возможное значение (up)

V_d – нижнее возможное значение (down)

Следовательно, стоимость позиции для фирмы может измениться в пределах от +51’250 евро, до -51’250 евро.

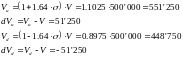
Рисунок 2. Прибыли/убытки в пределах доверительного интервала

«Основа» риска – волатильность будет одинаковой для всех фирм. Саму же величину подверженную риску, фирма подбирает индивидуально, поскольку индивидуальны

• стоимость позиции V; и

• уровень доверительного интервала k.

Подобный поход удобен. Можно выразить в евро, сколько «стоит» стандартное отклонение:

σ_$=500’000●0,0625=31 250 €

От этой суммы, пользуясь свойствами нормального распределения, всегда можно перейти к доверительному интервалу, умножая эту сумму, например, на 1.64. Наш интервал будет охватывать все значения от -51 250 евро до +51 250 евро.

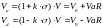
Если разделить VaR на рыночную стоимость портфеля, то получим величину потерь в процентах.

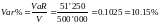
Краткосрочный актив

Рассмотрим для начала возможность применения формулы VaR для оценки величины возможных потерь в случае одного краткосрочного актива. Типичным примером может служить валютная позиция коммерческого банка. Банки отслеживают валютные позиции ежедневно, поэтому для однодневных колебаний валютного курса по валютам с глубоким рынком, во-первых, подходит предположение о нормальности движения курсов, а, во-вторых, по причине краткосрочности таких изменений мы можем абстрагироваться от параметра сдвига (дрейфа - μ), т.е. принять μ=0.

Отсюда следует, что наша позиция за один день может измениться следующим образом

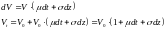
z – стандартный процесс Винера

Поскольку μ=0 и предполагается нормальность распределения в движении валютных курсов, мы можем утверждать, что величина, на которую может измениться наша позиция, с вероятность 68% окажется в диапазоне

где σ в данном случае – это однодневная волатильность.

Это и есть VaR, т.е. «стоимость» риска или величина возможных колебаний, выраженная в денежных единицах.

Эта формула является основой для последующих модификаций, которые часто встречаются при ее практическом использовании. Причем эти модификации достаточно просты при предпосылке о нормальности распределения.

Во-первых, предпосылка нормальности позволяет достаточно свободно перемещаться между различными доверительными интервалами. Поскольку дисперсия в случае нормального распределения стабильна, то легко перейти от 68%-го доверительного интервала к 95%-му интервалу, или, скажем, к 99%-му, что зависит от потребностей данного пользователя. Например, чтобы получить 95%-й доверительный интервал нужно формулу умножить на 1.64, а для 99%-го интервала коэффициент будет 2.33.

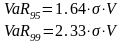
В общем случае

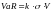
где k– соответствующий коэффициент перевода.

На практике финансисты по причине своей консервативности не удовлетворяются доверительным интервалом в 68%.

Во-вторых, нормальность распределения позволяет легко переходить в рамках данного доверительного интервала к различным временным интервалам. Волатильность при нормальном распределении изменяется по закону корня квадратного от времени. Поэтому, зная, например, однодневную волатильность курса доллара к евро, всегда можно рассчитать, скажем, 25-дневную волатильность, поскольку она равна 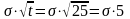. Значит, при увеличении временного интервала в 25 раз волатильность увеличится только в 5 раз.

В-третьих, если все рыночные факторы имеют нормальное распределение, то и их сумма также имеет нормальное распределение. Поэтому формула VaR для портфеля активов будет аналогична формуле VaR для отдельного актива. Различие только в том, что вариация должна относиться ко всему портфелю.

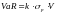
где σ_р – волатильность портфеля

Отсюда видно, что центральным звеном всего подхода является определение вариации и ковариации активов.

Таким образом:

1. для одного временного горизонта легко можно перейти от VaR для одного доверительного интервала к VaR для другого интервала (подбирая подходящий k);

2. для одного доверительного интервала всегда можно перейти к VaR с другим временным горизонтом (учитывая правило квадратного корня)

3. для одного доверительного интервала и одного временного горизонта всегда можно перейти от VaR для отдельных активов к VaR для их портфеля.

Таким образом, для оценки VaR важно знать распределение вероятностей и временной горизонт.

Пример. Портфель из одного актива

Немецкая компания ведет учет в евро, но имеет валютную позицию 120 млн. $.

Чему равен VaR на один день, если доверительный интервал 5%?

V=100 млн. €

σ=0,565%

€

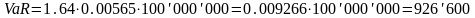Пример. Портфель из двух активов

Немецкая компания ведет учет в евро, но имеет позицию 120 млн. $ в американских T-bills.

Чему равен VaR на один день, если доверительный интервал 5%?

V=100 млн. €

σ_f=0,565%

σ_b=0,605%

ρ=-0.27

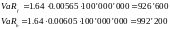
Это риски по отдельным позициям. Нам же нужно рассчитать риск по портфелю.

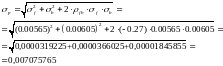
Следовательно,

€

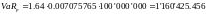Таким образом, для расчета VaR по валютным облигациям мы предварительно раскладываем позицию на элементарные составляющие. В качестве таких составляющих мы можем выделить валютный курс и набор казначейских облигаций. С другой стороны, можно представить эту же ситуацию в виде комбинации валютного курса и 120 млн. долларовых облигаций зеро. Тогда ценовой риск по облигации трансформируется в процентный риск, который сказывается на справедливой стоимости элементарной облигации.