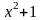Бинарные кодовые последовательности: код Лежандра.
Последовательность имеет длину N=4x+3
Построение последовательности.
записываем индексы.
находим разностное множество (D)
определяем квадратный вычет
кодируем.
Правило кодирования:
ставим 1, если индекс является квадратным вычетом
ставим -1, если индекс является квадратным невычетом
Например, пусть N=11
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
i2 (mod N) |
0 |
1 |
4 |
9 |
5 |
3 |
3 |
5 |
9 |
4 |
1 |
ui |
1 |
1 |
-1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
D={0,1,3,4,5,9} – разностное множество
Бинарные кодовые последовательности: код Якоби.
N=p1*p2 p2=p1+2
Un=1 если n=0
Un=-1 если n=0(mod p1)
Un=1 если n=0(mod p2)
Фи1(n)=
Фи2(n)=
n
GF(p1)
n GF(p2)
Пример p1=5 p2=7
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
-1 |
-1 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
-1 |
=1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
-1 |
GF(5)=(1,2,3,4,)
n |
1 2 3 4 |
0=2 |
2 4 3 1 |
|
4 1 3 2 |
n
n |
1 2 3 4 5 6 |
2 |
2 4 1 2 4 1 |
3 |
3 2 6 4 5 1 |
n |
6 2 1 4 5 3 |
Бинарные кодовые последовательности: код Хола.
Последовательность имеет длину N=4x2+27
Построение:
записываем индексы
находим примитивный элемент
вычисляем indΘi
кодируем
Правило кодирования:
-1, если i≡0
1, если indΘi=0,1,3 (mod 6) или 1,2,4 (mod 6) или2,3,5 (mod 6)
-1 иначе
Например, пусть N=31. Примитивный элемент θ=3(3 возводим в степень i и берем по mod 31). Кодирование по 1му правилу.
Индекс i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
θ |
3 |
9 |
27 |
19 |
26 |
16 |
17 |
20 |
10 |
30 |
28 |
22 |
4 |
12 |
5 |
indΘi |
30 |
24 |
1 |
18 |
20 |
25 |
28 |
12 |
22 |
21 |
6 |
7 |
26 |
4 |
8 |
код |
1 |
1 |
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
1 |
-1 |
1 |
-1 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
15 |
14 |
11 |
2 |
6 |
18 |
23 |
7 |
21 |
1 |
29 |
17 |
27 |
13 |
10 |
5 |
3 |
16 |
9 |
15 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
1 |
Бинарные кодовые последовательности: М-последовательность
=63
GF(2)
u-это
фи
GF
Мощность
метода кодирования будет равна этому
числу
Существует несколько эквивалентных способов построения последовательности:
1) на основе матрицы сопровождающей неприводимый многочлен
2)на
основе понятия следа GF(
)
3)на основе линейного рекуррентного уравнения
Пример (1 способ):
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
-1 |
1 |
1 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
|
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
|
=>
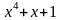(это будет последний столбец)
0001
A = 1001
0100
0010
Сдвиг на 4
2 способ:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
x |
x |
|
|
x+1 |
|
|
|
|
|
n |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
3 способ:
-
начальное состояние
i=n,
n+1,
…,
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |