Эцп на основе алгоритма Эль-Гамаля.
Параметры цифровой подписи:
1.Простое
число р; p>
;
2.Параметры эллиптической кривой (a, b);
3.m – порядок группы точек эллиптической кривой (иначе говоря, число точек);
4.Выбирается
простое число q – порядок циклической
подгруппы группы точек эллиптической
кривой, для которой должны выполняться
условия: m=n
q,
n
,
причем n - целое, 
.
5.Выбирается ненулевая точка эллиптической кривой Р(Хр;Ур);
Генерация ключей:
1.Выбирается случайное целое число d, 0<d<q; d – закрытый ключ;
2.Открытый
ключ: Q(Xq;Yq),
Q=d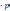
Алгоритм формирования цифровой подписи:
1.Вычисляется
значение хэш-функции открытого сообщения:
; e
= 
;
Если e=0, то e:=1;
2.Выбираем целое случайное число k, 0<k<q;
3.C(Xc;Yc); C=k P; (Вычисляется точка эллиптической кривой С); r=Xc(mod q);
4.S=(
)mod
q;
Если S=0,
то возвращаемся на шаг 2.
Параметры цифровой подписи: числа (r; S);
Алгоритм проверки цифровой подписи:
1.Проверяются условия 0<r<q; 0<S<q; Если хотя бы одно из условий не выполняется, то подпись отклоняется;
2.Вычисляется
значение хэш-функции
; e
=
;
Если e=0, то e:=1;
3.
;
4.
;
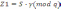Z2=-r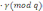
;
5.C(Xc;Yc);
;
R=Xc(mod q);
6.Если R=r, то подпись верна, и она принимается. Иначе подпись отклоняется
Простое поле Голуа.
Множество F с двумя бинарными операциями + и • называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению и выполняется свойство дистрибутивности.
Дистрибутивность – x•(y + z) = x•y + x•z
Ассоциативность – (x•y)•z = x•(y•z)
Коммутативность – x•y = y•x
Характеристика поля всегда 0 или простое число (n•1=0, n – хар-ка)
Поле характеристики 0 содержит Q, поле рациональных чисел.
Поле характеристики p содержит Zp, поле вычетов по модулю p.
Количество элементов в конечном поле всегда равно pn, степени простого числа.
При этом для любого числа вида pn существует единственное (с точностью до изоморфизма) поле из pn элементов, обычно обозначаемое Fpn.
Любой ненулевой гомоморфизм полей является вложением.
Примеры поля:
множества рациональных, вещественных, комплексных чисел.
Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов.
Обычно обозначается GF(p), где p — число элементов поля. Простое поле Галуа GF(p) = {S , ⊕ , ⊗} с бинарными операциями ⊕, ⊗.
Простейшим примером конечного поля является Zp — кольцо вычетов по модулю простого числа, где p – простое
Пусть надо построить поле GF(9) = GF(32). Для этого необходимо найти многочлен степени 2, неприводимый в Z3. Такими многочленами являются x2 + 1, x2 + x + 2, x2 + 2x + 2, 2x2 + 2, 2x2 + x + 1, 2x2 + 2x + 1.
Возьмем, например, x2 + 1, тогда искомое поле есть GF(9) = Z3[x]/<x2+1>. Если вместо x2 + 1 взять другой многочлен, то получится новое поле, изоморфное старому. Строятся таблицы умножения и сложения в поле GF(9).