
- •1)Свойства действительных чисел.
- •2)Свойства абсолютной величины действительного числа
- •4)Понятие сходящейся и расходящейся последовательности.
- •5)Теорема о предельном переходе в неравенстве.
- •6)Теорема о сжатой переменной (о трех последовательностях)
- •8)Теоремы о бесконечно малых.
- •10)Теорема Вейештрасса о последовательностях.
- •11)Определение числа е как предела последовательности.
- •12)Критерий сходимости последовательностей, основанный на поведении их подпоследовательностей. Лемма о вложенных промежутках.
- •13)Теорема Больцано-Вейерштрасса. Частичные пределы.
- •15)Критерий Коши сходимости последовательности. Примеры применения критерия.
- •16)Бесконечно большие последовательности. Их свойства. Примеры.
- •17)Понятие открытого, закрытого множеств, области на r, предельной точки множества. Примеры.
- •18)Теорема о равносильности 2-ч определений предела функции. Замечания.
15)Критерий Коши сходимости последовательности. Примеры применения критерия.
Теорема (критерий Коши): Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство. 1) Необходимость. Пусть последовательность {хn} сходится и х — ее предел. Требуется доказать, что эта последовательность является фундаментальной. Возьмем любое положительное число ε. Из определения сходящейся последовательности вытекает, что для положительного числа ε/2 найдется номер N такой, что при n≥ N выполняется неравенство \хn — х\ < ε/2.
Если р — любое натуральное число, то при n≥N выполняется также и неравенство \хn+p— х\ < ε/2. Так как модуль суммы двух величин не больше суммы их модулей, то из последних двух неравенств получим, что при n≥N и для всех натуральных чисел р
Тем
самым фундаментальность последовательности
{хn} установлена. ![]()
2)
Достаточность . Пусть {хn} — фундаментальная
последовательность. Требуется доказать,
что эта последовательность сходится.
Согласно теореме достаточно для этого
доказать ограниченность последовательности
{хn} и равенство ее верхнего и нижнего
пределов . Ограниченность фундаментальной
последовательности уже установлена
нами выше. Для доказательства равенства
верхнего и нижнего пределов воспользуемся
доказанным выше свойством фундаментальной
последовательности: для любого
положительного числа е можно указать
элемент xN
такой, что вне интервала (xN—
ε, xN+
ε) находится не более чем конечное число
элементов последовательности. Интервал
(xN—
ε, xN+
ε) содержит интервал ( ,
, ),
и поэтому
),
и поэтому
 –
– ≤ε,
откуда, в силу произвольности ε,
≤ε,
откуда, в силу произвольности ε, =
=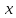 . Тем самым сходимость последовательности
установлена. Теорема полностью доказана.
. Тем самым сходимость последовательности
установлена. Теорема полностью доказана.
Пример.
Применим критерий Коши для установления
сходимости следующей последовательности
{xn}:
xn=a1+a2+a3+…+an
где ak
(к = 1,2,3,...) — произвольные вещественные
числа, удовлетворяющие условию \аk\ ≤ ,
a q — некоторое число из интервала 0 <
q < 1. Пусть n—
любой номер, р — любое натуральное
число. Тогда, очевидно,
,
a q — некоторое число из интервала 0 <
q < 1. Пусть n—
любой номер, р — любое натуральное
число. Тогда, очевидно,
![]()
Учитывая,
что последовательность { }
является бесконечно малой, можно
утверждать, что для любого ε > 0 найдется
номер N такой, что
}
является бесконечно малой, можно
утверждать, что для любого ε > 0 найдется
номер N такой, что![]() Стало
быть, при n≥N
и для любого натурального р
Стало
быть, при n≥N
и для любого натурального р![]() т.
е. последовательность {xn}
является фундаментальной и сходится
согласно теореме.
т.
е. последовательность {xn}
является фундаментальной и сходится
согласно теореме.
Пример:
Докажем, что
последовательность ![]() не
является фундаментальной.
не
является фундаментальной.
Покажем,
что ![]() расходящаяся
:
Рассмотрим последовательность
расходящаяся
:
Рассмотрим последовательность ![]() Доказательство
проведем методом от противного.
Предположим, что наша последовательность
фундаментальная, тогда по определению
фундаментальной последовательности:
Доказательство
проведем методом от противного.
Предположим, что наша последовательность
фундаментальная, тогда по определению
фундаментальной последовательности:
![]() поскольку
n и m любые, то возьмём
поскольку
n и m любые, то возьмём ![]() таких
слагаемых будет N штук, из всех слагаемых
таких
слагаемых будет N штук, из всех слагаемых ![]() —
наименьшее.
Можно сказать, что сумма
будет больше, чем сумма N наименьших
слагаемых, то есть:
—
наименьшее.
Можно сказать, что сумма
будет больше, чем сумма N наименьших
слагаемых, то есть:
![]() ,
а значит последовательность не является
фундаментальной.
Мы пришли к противоречию.
,
а значит последовательность не является
фундаментальной.
Мы пришли к противоречию.
16)Бесконечно большие последовательности. Их свойства. Примеры.
Определение. Последовательность {хn} называется бесконечно большой, если для любого положительного числа A (сколь большим бы его не взяли) можно указать номер N такой, что при n≥N все элементы хn этой последовательности удовлетворяют неравенству \хn\ > А.
Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной, поскольку для лю- любого А > 0 можно указать номер N такой, что при n > N все элементы хn удовлетворяют неравенству \хn\ > А, а следовательно, для любого А > 0 найдется по крайней мере один такой элемент xn, что \хn\ > А.
Теорема (о связи б.м.п. и б.б.п.) Если {хn} — бесконечно большая последовательность, то, начиная с некоторого номера n, определена по- последовательность {1/xn}, которая является бесконечно малой. Если все элементы бесконечно малой последовательности {аn} не равны нулю, то последовательность {1/аn} бесконечно большая.
Доказательство.
Пусть {xn}
– б.б.п, т.е. для любых
 ,
существует Nε
,
существует Nε ,
для любых n≥Nε,
│xn│≥ε.
Это означает, что n≥Nε
все элементы xn
,
для любых n≥Nε,
│xn│≥ε.
Это означает, что n≥Nε
все элементы xn ,
поэтому последовательность {1/xn}
имеет смысл начиная с некоторого номера
Nε.
Пусть А – любое положительное число,
тогда для числа 1/А существует N1
такое что для любых n≥N1
│1/xn│<A,
что по определению означает, что
последовательность {1/xn}
– бесконечно малая. Второе доказательство
проводится аналогично.
,
поэтому последовательность {1/xn}
имеет смысл начиная с некоторого номера
Nε.
Пусть А – любое положительное число,
тогда для числа 1/А существует N1
такое что для любых n≥N1
│1/xn│<A,
что по определению означает, что
последовательность {1/xn}
– бесконечно малая. Второе доказательство
проводится аналогично.
Свойства бесконечно больших последовательностей:
1)Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность того же знака.
Пусть ![]() —
бесконечно большие последовательности.
По
определению:
—
бесконечно большие последовательности.
По
определению:
![]() и .
и .
![]() Тогда
для последовательности
Тогда
для последовательности ![]() :
:
 ,
что означает, что последовательность
,
что означает, что последовательность ![]() —
бесконечно большая.
—
бесконечно большая.
2)Сумма бесконечно большой и ограниченной последовательностей есть бесконечно большая последовательность.
Пусть
последовательность ![]() —
бесконечно большая,
—
бесконечно большая, ![]() —
ограниченная. Тогда по определению
—
ограниченная. Тогда по определению ![]() и
и ![]() .
Рассмотрим
.
Рассмотрим ![]() :
:
 │=│xn│*(1+0)=│xn│≥ε
Получили:
│=│xn│*(1+0)=│xn│≥ε
Получили:  ,
что означает, что последовательность
,
что означает, что последовательность ![]() —
бесконечно большая.
—
бесконечно большая.
3)Произведение бесконечно больших последовательностей есть бесконечно большая последовательность. (Доказывается аналогично предыдущему)
4)Произведение
бесконечно большой последовательности
на константу есть бесконечно большая
последовательность.
Пусть
последовательность ![]() —
бесконечно большая,
—
бесконечно большая, ![]() —
константа. Тогда по определению
—
константа. Тогда по определению ![]() .
Рассмотрим
.
Рассмотрим ![]() :
:![]()
(по
теореме о связи между бесконечно большими
и бесконечно малыми последовательностями).
![]() —
константа,
—
константа, ![]() —
также константа, т.е. ограниченная.
{
—
также константа, т.е. ограниченная.
{ }={
}={ }
} ,
что означает, что последовательность
,
что означает, что последовательность ![]() —
бесконечно большая.
—
бесконечно большая.
Примеры:
-
Последовательность
 является
бесконечно большой, т.к.
является
бесконечно большой, т.к.  .
. -
Последовательность
 является
бесконечно большой, т.к.
является
бесконечно большой, т.к.  .
. -
 —
бесконечно большая,
т.к.
—
бесконечно большая,
т.к.  ,
а
,
а  —
ограниченная, сохраняющая знак.
—
ограниченная, сохраняющая знак.
