10)Теорема Вейештрасса о последовательностях.

*Определение. Последовательность {х_n} называется неубывающей (невозрастающей), если каждый последующий член этой последовательности не меньше (не больше) предыдущего, т. е. если для всех номеров n справедливо неравенствоx_n ≤x_n+1 (x_n ≥x_n+1 ). Монотонные последовательности ограничены либо сверху, либо снизу. Именно: невозрастающие последовательности ограничены сверху, а неубывающие последовательности ограничены снизу своими первыми элементами. Поэтому невозрастающая последовательность будет ограниченной с двух сторон, если она ограничена снизу, а неубывающая последовательность будет ограниченной с двух сторон, если она ограничена сверху.

*Теорема . Если неубывающая (невозрастающая) последовательность {х_n} ограничена сверху (снизу), то она сходится.

Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости.

Теорема Вейерштрасса об ограниченной сверху возрастающей последовательности (или ограниченной снизу убывающей последовательности) утверждает, что любая ограниченная сверху монотонно возрастающая (или ограниченная снизу монотонно убывающая) последовательность имеет предел, причем этот предел равен её точной верхней (или нижней) грани.

Пусть {\displaystyle {x_{n}}}{x_n} - ограниченная возрастающая последовательность. Cледовательно, по теореме о супремуме, имеет супремум. Обозначим его через {\displaystyle S}S. Тогда  {\displaystyle \lim _{n\to \infty }x_{n}=S}. Действительно, так как {\displaystyle S}S — супремум множества {\displaystyle \{x_{n}\}_{n\in \mathbb {N} }}{x_n}, то для любого {\displaystyle \varepsilon >0}ε существует номер {\displaystyle N}N такой, что {\displaystyle S-\varepsilon <x_{N}\leqslant S}S-ε_N≤S. Тогда для любого {\displaystyle n>N}n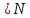 имеем: S-ε_N≤x_n≤S {\displaystyle S-\varepsilon <x_{N}\leqslant x_{n}\leqslant S}. Тогда {\displaystyle \left|{x_{n}-S}\right|<\varepsilon }│x_n-S│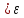 при {\displaystyle n>N}n. Следовательно, {\displaystyle \lim _{n\to \infty }x_{n}=S} Теорема доказана.

11)Определение числа е как предела последовательности.

Применим теорему Вейерштрасса о существовании предела монотонной последовательности для доказательства существования предела последовательности {x_n}, элемент х_n которой определяется формулой .

Докажем, что эта последовательность возрастает и ограничена сверху. Применив формулу бинома Ньютона, найдем

Представим это выражение в следующей форме:

1. 

Аналогично запишем элемент x_n+1 :

Сравнивая два выражения получаем , что x_n x_n+1 , т.е. последовательность {x_n} возрастающая.

Для доказательства ограниченности этой последовательности сверху заметим, что каждое выражение в круглых скобках в соотношении 1) меньше единицы. Учитывая также, что , при к ≥2 получим

Итак, последовательность {x_n} возрастает и ограничена сверху. По теореме Вейерштрасса последовательность {x_n} имеет предел. Этот предел по определению называют числом е . Следовательно по определению = e. (e =2,71828)