4)Понятие сходящейся и расходящейся последовательности.

Последовательность {х_n} называется сходящейся, если существует такое число а, что для любого положительного числа можно указать номер N такой, что при n≥N все элементы х_n этой последовательности удовлетворяют неравенству \х_n-а\<.

При этом число а называется пределом последовательности {х_n}.

Последовательность {х_n} называется сходящейся, если существует число а такое, что в любой -окрестности числа а находятся все элементы последовательности {x_n}, начиная с некоторого номера. (-окрестностью числа а называется интервал 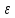(a —, a + )).

Числовая последовательность не имеющая предела называется расходящейся.

Пример: последовательность 1,-1,1… - расходящаяся ;

2. Основные свойства сходящихся последовательностей.

Теорема : Сходящаяся последовательность имеет только один предел.

Дказательство: Пусть а и b — пределы сходящейся последовательности {x_n}. Тогда, для элементов х_n сходящейся последовательности {х_n}, получим х_n = а + а_n, х_n = Ь + b_n, где а_n и b_n — элементы бесконечно малых последовательностей {а_n} и {b_n}. Вычитая написанные соотношения, найдем a_n – b_n= Ь - a. Так как все элементы бесконечно малой последовательности {а_n —b_n} имеют одно и то же постоянное значение b — а, то b— а = 0, т. е. b = а. Теорема доказана.

Теорема : Сходящаяся последовательность ограничена.

Доказательство. Пусть {х_т} — сходящаяся последовательность и а — ее предел. Тогда, существует ε, N(ε): при,  ,. Тогдадляn.

5)Теорема о предельном переходе в неравенстве.

Теорема: Если элементы сходящейся последовательности {х_n}, начиная с некоторого номера, удовлетворяют неравенству х_n ≥b(х_n ≤ Ь), то и предел а этой последовательности удовлетворяет неравенству а≥b (а≤b).

Доказательство: Пусть все элементы x_n, начиная с некоторого номера, удовлетворяют неравенству Х_n ≥ Ь. Требуется доказать неравенство а ≥Ь. Предположим, что а < Ь. Поскольку а — предел последовательности {x_n}, то для положительного ε = Ь — а можно указать номер N такой, что при n≥ N выполняется неравенство \хп — а\ < Ь — а. Это неравенство эквивалентно следующим двум неравенствам: — (Ь — а) < хп — а < Ь — а. Используя правое из этих неравенств, получим х_n < Ь, а это противоречит условию теоремы.

Замечание. Элементы сходящейся последовательности {х_n} могут удовлетворять строгому неравенству х_n > b, однако при этом предел а может оказаться равным b. Например, если х_n = , то х_n > 0, однако.

Следствие 1. Если элементы х_n и у_n сходящихся последователъностей {х_n} и {у_n}, начиная с некоторого номера, удовлетворяют неравенству х_n , у_n, то их пределы удовлетворяют такому же неравенству: .

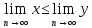Следствие 2. Если все элементы сходящейся последовательности {х_n} находятся на сегменте [а,Ь], то и ее предел с также находится на этом сегменте.

6)Теорема о сжатой переменной (о трех последовательностях)

Теорема: Пусть {х_n} и {z_n} — сходящиеся последовательности, имеющие общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {у_n} удовлетворяют неравенствам х_n ≤ у_n ≤ z_n. Тогда последовательность {у_n} сходится и имеет предел а.

Доказательство. Достаточно доказать, что последовательность {у_n — а} является бесконечно малой. Обозначим через N* номер, начиная с которого выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполняться также неравенства х_n — а ≤у_n — а ≤z_n-a. Отсюда следует, что при n ≥ N* элементы последовательности {y_n — a} удовлетворяют неравенству │y_n –a │≤max{│x_n -a│,│z_n-a│}.Так как и , то для любого ε> 0 можно указать номера N₁ и N₂ такие, что при n≥ N₁ \x_n - a\ < ε, а при n≥ N₂ \z_n — а\ < ε. Пусть N = max{N*, N₁, N₂}. Начиная с этого номера, имеет место неравенство \уп ^ а\ < ε. Итак, последовательность {у_n –а} — бесконечно малая. Теорема доказана:)

7)Теорема о стабилизации знака.

Теорема: Пусть {x_n} сходящаяся последовательность , предел которой равен а; а. Тогда начиная с некоторого номера n , переменная x_n.

Докозательство:Пусть . Предположим ε=a-p . По определению предела последовательности для этого ε найдется К_ε N такое, что К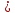К_ε и│х_к-а│ε. Т.е при любых КК_ε , число х_к удовлетворяет неравенствам а-εх_ка+ε. Но а-ε=а-(а-р)=р, значит, КК_ε и рх_к . Предположим К_р = К_ε . Тогда при всех КК_р справедливо px_k . Ч.и.т.д