8)Теоремы о бесконечно малых.

Теорема: Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство. Пусть {а_n} и {b_n} — бесконечно малые последовательности. Докажем, что последовательность {a_n +b_n}— бесконечно малая. Пусть ε — произвольное положительное число, N₁— номер, начиная с которого \а_n\ < ε/2, а N₂ — номер, начиная с которого \b_n\ < ε/2. (Такие номера N₁ и N₂ найдутся по определению бесконечно малой последовательности.) Так как модуль суммы двух чисел не превосходит суммы их модулей, т. е. \а_n+ b_n\ ≤\а_n\ + \b_n\ , то, обозначив через N наибольший из двух номеров N₁ и N₂, мы получим, что, начиная с номера N, выполняется неравенство \а_n + b_n\ < ε. Это означает, что последовательность {а_n + b_n} бесконечно малая. Теорема доказана.

Теорема: Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Эта теорема доказывается аналогично предыдущей, только вместо неравенства \а_n + b_n\ ≤ |а_n| + \b_n\ следует взять неравенство \а_n — b_n\≤\а_n\ + \b_n\.

Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей — бесконечно малая последовательность.

Теорема: Бесконечно малая последовательность ограничена.

Доказательство. Пусть {а_n} — бесконечно малая последовательность и ε - некоторое положительное число. Пусть, далее, N — номер, начиная с которого \а_n\ < ε. Обозначим через А наибольшее из следующих N чисел: ε, |a₁|, |а₂|,..., │a_N -1│.Это можно записать так: А = mах{ε, |a₁ |, |a₂|,…, |a_N -1|} . Очевидно, \а₂\ ≤А для любого номера n , что означает ограниченность последовательности. Теорема доказана.

Теорема: Произведение ограниченной последовательности на бесконечно малую последовательность представляет собой бесконечно малую последовательность.

Доказательство. Пусть {х_n} — ограниченная , а {a_n} — бесконечно малая последовательности. Так как последовательность {х_n} ограничена, то существует число А > 0 такое, что любой элемент х_n удовлетворяет неравенству \х_n\ ≤А. Возьмем произвольное положительное число ε. Поскольку последовательность {а_n} бесконечно малая, то для положительного числа ε/А можно указать номер N такой, что при n≥N выполняется неравенство \a_n\ < ε/А. Тогда при n≥ N \ х_n*a_n\ = \х_n\ * \а_n\ < А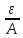 = ε. Поэтому последовательность {х_n * а_n} бесконечно малая. Теорема доказана.

Следствие. Произведение любого конечного числа бесконечно малых последовательностей представляет собой бесконечно малую последовательность.

Замечание. Частное двух бесконечно малых последовательностей может быть последовательностью любого типа и даже может не иметь смысла.

Теорема. Если все элементы бесконечно малой последовательности {а_n} равны одному и тому же числу с, то с = 0.

Докозательство: Пусть . Тогда для . По условию, , тогда . Получили противоречие, следовательно, .

9)Теоремы об арифметических действиях над сходящимися последовательностями.

Теорема . Сумма сходящихся последовательностей {х_n} и {у_n} есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {х_n} и {у_n}.

Доказательство. Пусть а и b — соответственно пределы последовательностей {х_n} и {у_n}. Тогда х_n = а + а_n и y_n = Ь + b_n, где {а_n} и {b_n} — бесконечно малые последовательности. Следовательно, (х_n + у_n) - (а + Ь) = а_n + b_n. Таким образом, последовательность {(х_n+у_n) — (а+Ь)} бесконечно малая, и поэтому последовательность {х_n + у_n} сходится и имеет своим пределом число а + Ь.

Теорема . Разность сходящихся последовательностей {х_n} и {у_n} есть сходящаяся последовательность, предел которой равен разности пределов последовательностей {х_n} и {у_n}.

Доказательство этой теоремы аналогично доказательству теоремы о сумме.

Теорема 3.11. Произведение сходящихся последовательностей {х_n} и {у_n} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {х_n} и {у_n}.

Доказательство. Если а и b — пределы последовательностей {х_n} и {у_n} соответственно, то х_n = а + а_n, у_n = b + a_n и х_n * y_n = а*b + а*b_n + b*a_n +a_nb_n. Следовательно, х_n * у_n - а *b = а*b_n + b*a_n +a_nb_n. В силу теоремы о бесконечно малых и следствия из нее, { а*b_n + b*a_n +a_nb_n } бесконечно малая, т. е. и последовательность {хп - уп — а - Ь} бесконечно малая, и поэтому последовательность {хп • уп} сходится и имеет своим пределом число а • Ь.

Лемма . Если последовательность {у_n} сходится и имеет отличный от нуля предел Ь, то, начиная с некоторого номера, определена последовательность { , которая является ограниченной.

Доказательство. Пусть е = | Ь |/2. Так как b≠0, то е > 0. Пусть N — номер, соответствующий этому е, начиная с которого выполняется неравенство | у_n — b│ < е или │y_n -Ь│ < │Ь│/2. Из этого неравенства следует, что при n≥N выполняется неравенство │у_n│> │Ь│/2. Поэтому при n≥N имеем ││<. Следовательно, начиная с этого номера N, мы можем рассматривать последовательность { и эта последовательность ограничена. Лемма 1 доказана.

Теорема. Частное двух сходящихся последовательностей {х_n} и {у_n} при условии, что предел {у_n} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {х_n} и {у_n}.

Доказательство. Из доказанной леммы 1 следует, что, начиная с некоторого номера N, элементы последовательности {у_n} отличны от нуля и последовательность { ограничена. Начиная с этого номера, мы и будем рассматривать последовательность { . Пусть а и b — пределы последовательностей {х_n} и {у_n}. Докажем, что последовательность{ бесконечно малая. В самом деле, так как х_n = а + a_n , у_n = b +b_n то =.Так как последовательность { ограничена, а последовательность бесконечно малая, то последовательность {}≡бесконечно малая. Теорема доказана.