
- •1)Свойства действительных чисел.
- •2)Свойства абсолютной величины действительного числа
- •4)Понятие сходящейся и расходящейся последовательности.
- •5)Теорема о предельном переходе в неравенстве.
- •6)Теорема о сжатой переменной (о трех последовательностях)
- •8)Теоремы о бесконечно малых.
- •10)Теорема Вейештрасса о последовательностях.
- •11)Определение числа е как предела последовательности.
- •12)Критерий сходимости последовательностей, основанный на поведении их подпоследовательностей. Лемма о вложенных промежутках.
- •13)Теорема Больцано-Вейерштрасса. Частичные пределы.
- •15)Критерий Коши сходимости последовательности. Примеры применения критерия.
- •16)Бесконечно большие последовательности. Их свойства. Примеры.
- •17)Понятие открытого, закрытого множеств, области на r, предельной точки множества. Примеры.
- •18)Теорема о равносильности 2-ч определений предела функции. Замечания.
Билеты. Высшая математика.
1)Свойства действительных чисел.
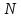 ⊂
⊂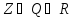
N – множество натуральных чисел (1,2,…,+∞)
Z – множество целых чисел (-∞,+∞)
Q
– множество рациональных чисел (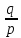 )
, q
)
, q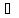 Z,
p
Z,
p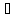 Z
Z
R – множество действительных (вещественных) чисел; множество всевозможных, бесконечных десятичных дробей
Вещественные числа, не являющиеся рациональными, называют иррациональными.
①
-
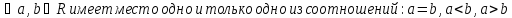
-
a
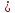 b
, b
b
, b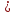 c
c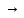 a
a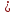 c
(транзитивное свойство знака
c
(транзитивное свойство знака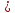 )
) -
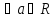 существует m
существует m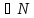 ,
такое что
,
такое что
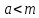 (аксиома
Архимеда)
(аксиома
Архимеда)
② a+b комутативная группа по сложению
-
Комутативность: a+b=b+a
-
Ассоциативность: a+(b+c)=a+b+c
-
Наличие нейтрального члена: a+0=0+a=a
-
Наличие противоположного члена: a+b=1; b=-a
-
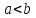
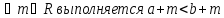
③a*b комутативная группа по умножению
-
Комутативность: a*b=b*a
-
Ассоциативность: a*(b*c)=a*b*c
-
Наличие нейтрального члена: a*1=1*a=a
-
Наличие противоположного члена: a*b=1; b=1/a
-
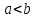

④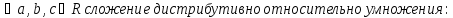
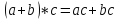
⑤
-
R – плотное множество. Между любыми двумя различными числами a и b существует бесконечное множество действительных чисел.
-
Множество R непрерывно(теорема Дедекинда)
Пусть A и B — два непустых множества в R таких, что ∀a ∈ A ∀b ∈ B a ≤ b, т. е. любой элемент A не больше любого элемента B. Тогда ∃c ∈ R | ∀a ∈ A ∀b ∈ B a ≤ c ≤ b, т.е. найдется хотя бы одно число, разделяющее A и B
2)Свойства абсолютной величины действительного числа
Абсолютной величиной (модулем) действительного числа х (обозначается │х│) называется неотрицательное действительное число, удовлетворяющее условиям:

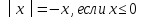
Свойства:
1)Абсолютная величина алгебраической суммы нескольких действительных чисел не больше абсолютных величин слагаемых:
│a+b│≤│a│+│b│
2)Абсолютная величина разности не меньше разности абсолютных величин уменьшаемого и вычитаемого:
│a-b│≥│a│-│b│ (│a+b│≥│a│-│b│)
3) │ab│≤│a││b│
4) │a/b│≤│a│/│b│
Докозательство:
сложим почленно неравенства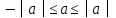 и
и

 и получаем
│a+b│≤│a│+│b│;
если заменить b
на –b
то получим│a-b│≤│a│+│b│
и получаем
│a+b│≤│a│+│b│;
если заменить b
на –b
то получим│a-b│≤│a│+│b│
3)Ограниченные множества и их границы. Понятие счетного и несчетного множества. Примеры.
Если каждому числу п натурального ряда чисел 1,2,... n, ... ставится в соответствие по определенному закону некоторое вещественное число xn то множество занумерованных вещественных чисел x1,x1,...,xn,… мы и будем называть числовой последовательностью или просто последовательностью.
Определение 1. Последовательность {хn} называется ограниченной сверху (с н и з у), если существует такое вещественное число М (число га), что каждый элемент хn последовательности {хn} удовлетворяет неравенству хn ≤М (хn ≥m).
При этом число М (число m) называется верхней гранью (нижней гранью) последовательности {xn}, а неравенство Xn ≤ М (хn ≥m) называется условием ограниченности последовательности сверху (снизу). Любая ограниченная сверху последовательность {хn} имеет бесчисленное множество верхних граней. Если М — верхняя грань, то любое число М*, большее М, также является верхней гранью.
Определение 2. Последовательность {хn} называется ограниченной с обеих сторон или просто ограниченной, если она ограничена и сверху, и снизу, т. е. если существуют числа m и М такие, что любой элемент хп этой последовательности удовлетворяет неравенствам: m≤хn ≤М.
Наименьшая верхняя граница называется также точной верхней границей A, верхней гранью A или супремумом A и обозначается sup A. Наибольшая нижняя граница называется также точной нижней границей A, нижней гранью A или инфимумом A и обозначается inf A
Последовательность {хn} называется неограниченной, если для любого положительного числа А найдется элемент хn этой последовательности, удовлетворяющий неравенству │хn│ > А.
Рассмотрим несколько примеров:
1)Последовательность —1, —4, —9, ... , n2, ... ограничена сверху и не ограничена снизу. Верхней гранью этой последовательности является любое число, не меньшее — 1.
2)Последовательность 1, 1/2, 1/3, ... , 1/n, ... ограничена. Действительно, верхней гранью этой последовательности является любое число М ≥1, а нижней гранью — любое число m≤0.
Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если каждому элементу множества A соответствует один и только один элемент множества B и каждому элементу множества B соответствует некоторый элемент множества A. В этом случае говорят также, что множества A и B изоморфны .
Два множества A и B называются эквивалентными, или равномощными, если между этими множествами может быть установлено взаимно однозначное соответствие и говорят, что множества A и B имеют равные мощности.
Множество A называется конечным, если оно эквивалентно Jn при некотором n, где Jn=1, 2, …, n – множество n первых натуральных чисел. Множества, которые не являются конечными, называются бесконечными. Если некоторое множество A равномощно множеству натуральных чисел N, т.е. AN, то множество A называется счетным. Счетное множество A – это такое множество, все элементы которого могут быть занумерованы в бесконечную последовательность a1, a2, …, an, …, так, чтобы при этом каждый элемент получил лишь один номер n и каждое натуральное число n было бы номером лишь одного элемента множества A.
Множество А [0,1] несчетное множество ; множество Q счетное множество
